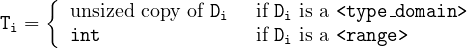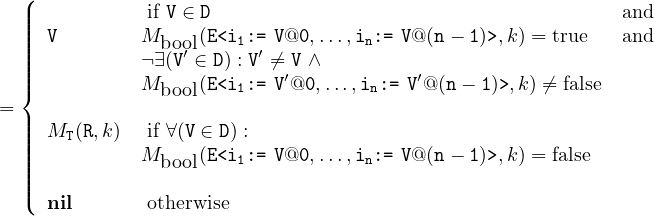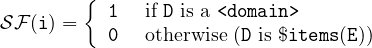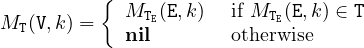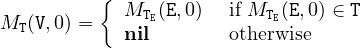HLL
Language Definition
Date: June 16, 2022
Version: 3.2
Legal Notice
No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in
any form or by any means, without the inclusion of the front-page, nor without the
inclusion of the present page which includes this legal notice and the history section
below.
The authors and the copyright holders of this document make no warranties, neither
expressed nor implied, regarding this document or the subject matter described herein,
including, but not limited to, warranties of merchantability or fitness for any particular
purpose.
While considerable efforts have been made to assure the accuracy of this document and the
matter it describes, the authors and the copyright holders will in no event assume
responsibility for any direct, indirect, special, incidental or consequential damages resulting
from any errors or omissions in the document, including loss of life. The contents of this
document may be changed without prior notice.
History
The language HLL was developed by Prover Technology (Prover) from 2008 to 2012 in
collaboration with RATP. The language emerged as a successor of the TeclaTool language,
which itself was a successor of the Tecla language, both developed by Prover before
2008.
In 2018, HLL 2.7 Logical Foundations Document (LFD) was published on the Internet [1].
Prover renamed and profoundly rewrote the LFD in order to organize it in a more modular
way (all aspects of each language construct being grouped together in a single module) with
the main purpose of making it easier to ensure the completeness of the language
definition. The result was version 3.0 of the document with the new title “HLL Language
Definition”.
In 2018 the HLL Forum initiative started as a working group of tool providers and users of
HLL. The new features of HLL 3.0 (compared to version 2.7) were developed jointly by the
HLL Forum.
Author
Lars Helander, Prover Technology SAS.
Authors of previous versions
The present document has been based on previous language specifications.
- The document “Tecla LFD”, 2008, Prover Technology AB, defined the semantics
of streams and was written by Gunnar Smith and Ilya Beylin.
- The document “HLL LFD”, versions 1.0 to 2.7, 2012, Prover Technology SAS,
defined previous versions of HLL and was written by Nicolas Breton and Jean-Louis
Colaço.
Revision History
In the following table, revisions marked with a star have been approved.
| Version | Date | Reason for change |
| | |
|
| 3.2* | June 16, 2022 | This version is identical to 3.2rc1 (which
was accepted by technical review 11755)
except for the version number and this
entry in the revision history. |
| 3.2rc1* | May 13, 2022 | Minor change to the lexical structure
concerning carriage return and the null
character. Clarified that the membership
operator is left-associative. |
| 3.1* | March 31, 2022 | This version is identical to 3.1rc1 (which
was accepted by technical review 11615)
except for the version number and this
entry in the revision history. |
| 3.1rc1* | March 23, 2022 | Addressed issues arising from technical
review 11455. Added (CastNamedType)
which was missing. Also fixed minor issue
11578 and major issue 11478 concerning
the value nil in
domains (affecting (DomainAsRange) and
(Membership) and leading to the new
restriction (QuantDomainNotNil)). |
| 3.0rc11 | February 4, 2022 | Added a missing reference to the new
Appendix C. |
| 3.0rc10 | July 5, 2021 | Removed (QuantMinMaxDomainNonEmpty) and added nil-behaviour
instead for these quantifiers in case the
domain is empty. Minor fix regarding
the semantics of the domain of SELECT:
it is static due to the new restriction
(SelectQuantNoItemsDomain). Specified
that line-ending comments and pragmas
(//, @) are ended by the ’∖n’-character.
Added (CollectionStaticFlag)
which was missing. Changed the syntax
of <quantif_expr> by refactoring out the
SELECT case and accordingly removed the
restriction (QuantRestrictedDefault) which is no longer needed,
and renamed (QuantDefault) as (QuantSelectDefault).
Added Appendix C with an overview of
restrictions. Plus some other minor fixes
and clarifications. |
| 3.0rc9 | February 15, 2021 | Added authors on page 2. Marked version
3.0rc8 as approved (by the technical
reviewers). Added Appendix E with
contact details. Changed the document id
from T-810712-LFD-HLL to HLL-LDD. |
| 3.0rc8* | January 20, 2021 | Forbid the combination of SELECT and
$items by introduction of the restriction
(SelectQuantNoItemsDomain). Modified
(DefDeclaredLhsAssignableRhs) and renamed it
(DefRhsTypeAssignableToLhsType).
Minor addition to (DefCollectionRhs)
regarding the type of collections. Also
addressed issues arising from technical
review 10609. |
| 3.0rc7 | November 18, 2020 | Removed the appendix containing the type
system. Updated the semantics of branch
variables of case expressions (they are now
static streams). This fixes issue 10587.
Make undeclared and defined variables
default to type bool if they are defined
using a recursion. Updated the typing
of untyped PRE expressions. Simplified
the causality restriction for definitions.
Updated the type of the SELECT to be the
union type of the types of the selected value
and the default value (issue 10215). Plus
some minor clarifications. |
| 3.0rc6 | February 28, 2020 | Updated (QuantVarStaticFlag) due to the
introduction of $items. |
| 3.0rc5 | December 3, 2019 | Provided more details for the causality
restriction (DefCausality). Clarified the
typing of untyped pre expressions. Adding a
definition of the many-sorted model. Also
added the new features agreed upon by the
HLL forum. That is:
-
1.
- Unfolding definitions.
-
2.
- SELECT operator (as a quantifier
expression).
-
3.
- A <domain> is allowed to be
just "bool" or "int". (The other
extensions on this point having
already been added in a previous
version.)
-
4.
- Quantification (including SELECT)
over composite streams.
-
5.
- Arrays and functions as proof
obligations.
-
6.
- Extended integer literals (binary and
hexadecimal, plus underscores for
readability).
-
7.
- Always definitions aligned with latch
definitions for integer streams (added
a check that the value fits in the
target type).
-
8.
- A new Section 2.2: Logic of
Exceptions.
|
| 3.0rc4 | January 23, 2019 | Addressed issues arising from technical
review 9089. Redefined $or so that it does
not absorb nil. |
| 3.0rc3 | September 24, 2018 | Addressed issues arising from technical
review 8986. |
| 3.0rc2 | September 7, 2018 | Addressed issues arising from technical
review 8868. |
| 3.0rc1 | July 17, 2018 | Included a type system in appendix. |
| 3.0a | March 8, 2018 | Rewritten from scratch with another document
structure. Notable changes and additions to
HLL include:
-
1.
- Added an order on the values of the
bool, enum and integer types.
-
2.
- Functions over ordered domains are
now generalized arrays, and can be
used whenever arrays can.
-
3.
- Function types are compatible and
assignable only if their parameter
types are equal (same sets of values).
(Issue 1251.)
-
4.
- Empty arrays are allowed.
-
5.
- Empty integer range types are
allowed.
-
6.
- Equality and non-equality operators
extended to allow any pair of
objects with finite number of scalar
components.
-
7.
- Membership/elementhood extended
to allow any scalar type as domain.
-
8.
- Added nil as an exceptional value
and defined its sources (divisions by
zero, array indexing out of bounds,
overflows, et.c.) and its propagation
(can be absorbed by if-then-else,
case, and some Boolean operators
and quantifiers).
-
9.
- Streams of empty type (including
inputs and memories) are now in
principle allowed, but such a stream
will carry nil in each time step.
-
10.
- Removed the “sized” restriction on
pre expressions.
|
| 2.8 | February 21, 2014 | issues: 3987. Fix definition of dependency
relation for pre. Move misplaced sentence
in same subsection. Update the rule
references in the text following the
enumerated list in the definition of the
dependency relation. |
| 2.7* | March 13, 2012 | issues: 262. Add missing case for collections
in functions defined on types. |
| 2.6 | February 24, 2012 | issues: 1243, 1244. Modification of the
typing rule (case) to forbid multiple
occurrence of the same variable in a
pattern. Fix rule (c-definition), was two
restrictive the assignability condition was
missing. |
| 2.5 | February 1, 2012 | Add a missing check on rules for quantifiers
(no simultaneous multi-introduction of
an identifier in the scope). Revisit the
other rules that already defined this check
(lhs-iterators, lhs-parameters, lambda par
function and lambda par array). Reorder
items in the definition of H in rule system.
Add a missing condition on memories and
inputs about empty sorts. |
| 2.4 | December 19, 2011 | New syntax for the with (issue: 1063),
Integration of RATP remarks given in
FA_12_LFD-HLL_AQL-Prover_03,
reorganization of the syntax, introduction
of lambda definitions, some precisions
about array projection and function
application. Issue 1127 |
| 2.3 | August 23, 2011 | Integration of RATP remarks given in
FA_Qualif_v04_LFD-HLL_AQL-Prover_01 |
| 2.2 | May 17, 2011 | Issues: 237, 239, 241, 245, 247, 248, 249,
250, 251, 252, 254, 256, 257, 258, 259, 260,
261, 263, 264, 265, 267, 268, 271, 272, 273,
274, 275, 276, 277, 278, 280, 281 |
| 2.1 | April 28, 2011 | Issues: 157, 126, 125, 123, 122, 121, 120,
119, 117, 115, 114, 113, 112, 111, 103, 104,
105, 106, 107, 87, 90, 91, 93 |
| 2.0 | February 28, 2011 | Major extension of the language with:
quantifiers, pre, namespaces, functions,
sorts and new switch-case. |
| 1.16 | November 4, 2010 | Improvement of the postfix array type
notation specification. |
| 1.15 | October 27, 2010 | Fix BNF, the terminating ”s” was missing
for the keyword ”obligations”. |
| 1.14 | September 20, 2010 | Change static flag for cast; this operator
is not consider as static anymore. Change
the semantics of memories constrained by
an implementation type, the implicit cast
is removed. |
| 1.13 | January 18, 2010 | Add a comment to the typing rule of
definitions, as recommended by RATP in
FA-03_LFD-HLL_rqs_RATP. |
| 1.12 | December 30, 2009 | Integration of RATP
remarks in FA-03_LFD-HLL_rqs_RATP.
Modification of the syntax to allow
uncapitalised section names, as raised by
the parser review. |
| 1.11 | November 12, 2009 | Minor spelling corrections. |
| 1.10 | October 5, 2009 | Adding missing rules for type
int and collections. Fix the constraints in
rules (int-signed) and (int-unsigned), were
shifted. |
| 1.9 | September 14, 2009 | Introduction of tags for the requirements.
Fixes of issues found by the validation
activity. Revisit the typing rule (Case
with Default) to make explicit that
cases values are pairwise different. Fix
(array-declaration) rule, sizes must be
constant. |
| 1.8 | June 8, 2009 | Introduction of tags for the requirements.
Fixes of issues found by the validation
activity. |
| 1.7 | April 17, 2009 | Modification of the semantics of integer
memories, it depends now on the way it
is declared (a range or an implementation
type). Improvement of the presentation of
integer types. Integration of the feedbacks
from the approbation team (iteration 3). |
| 1.6 | April 7, 2009 | change the associativity of the power
operator, now it associates to the right. |
| 1.5 | April 7, 2009 | Integration of the feedbacks from the
approbation team (iteration 2). |
| 1.4 | April 4, 2009 | Integration of the feedbacks from the
approbation team. |
| 1.3 | March 30, 2009 | Fix typos, revisit the section about other
static checks. |
| 1.2 | March 27, 2009 | Fix a lot of typos found by peer review. |
| 1.1 | March 20, 2009 | Remove operator ← (left implication)
Change the associativity of i →, now it
is right associative. Complete the HLL
semantics. |
| 1.0 | March 19, 2008 | Initial Version. |
Contents
1 Introduction
This document presents the syntactical and semantical aspects of the
HLL
modelling language.
HLL is a declarative stream-based language with a large panel of types and operators. It is
suitable for modelling discrete-time sequential behaviours and expressing temporal properties
of these behaviours.
1.1 Purpose
The purpose of the document is to provide a formal definition of all aspects of HLL in order
to be used for the implementation of tools considering this language as a source or a
target.
This document is not intended as a user’s guide or introduction to HLL.
1.2 Definitions, Terms and Abbreviations
Please refer to Appendix D.
1.3 Overview
- Section 2 introduces the basic concepts, notions and notation on which the
remainder of the document rests, and should be read first of all.
- Section 3 describes the lexical structure of HLL, including comments and pragmas.
-
Section 4 to Section 16 describe the semantics and restrictions of the HLL language
around its EBNF syntax definition.
- Section 4 describes identifiers.
- Section 5 describes user namespaces and path identifiers.
- Section 6 describes lists.
- Section 7 describes declarators.
- Section 8 describes types.
- Section 9 describes accessors.
- Section 10 describes stream expressions.
- Section 11 describes stream declarations.
- Section 12 describes stream definitions.
- Section 13 describes constants.
- Section 14 describes constraints.
- Section 15 describes proof obligations.
- Section 16 describes sections.
The top-level nonterminal <HLL> that characterizes an HLL text is defined in Section 16
(the sections above have been ordered mostly bottom-up, with the top-level
last).
- Appendix A gives the complete ENBF syntax definition in a single place, for an
overview of the language, together with the operator precedence and associativity rules
in A.1.
- Appendix B lists the reserved words of HLL.
- Appendix C gives an overview of the different restrictions that apply to each language
construct of HLL.
- Appendix D is a glossary of words, terms and abbreviations used within this
document.
- Appendix D gives an index of (external) labels exported by this document.
- Appendix E provides information on how to contact Prover Technology.
2 Preliminaries
2.1 Streams
HLL is a language based on the notion of Streams. A stream s represents an infinite sequence
of values, one for each time step:
s : s0 s1 s2 s3 … sn sn+1 …
Streams are typed, and the type of a stream can be understood as just a set of values. For
example the Boolean type (written bool in HLL) is the set of values {false,true}.
The values si of the stream s are thus members of the type of s. HLL supports a
large number of different types, for example Boolean, integer, enum, struct and
array.
In HLL, there are two fundamentally different types of operators:
-
1.
- combinatorial operators (which are mappings from values to values), and
-
2.
- temporal operators (which are mappings from streams to streams).
The combinatorial operators that can be applied to values of a type T can be lifted to streams
of type T by point-wise application in each time step. For example, if a and b are integer
streams:
a : a0 a1 a2 … an …
b : b0 b1 b2 … bn …
Then the expression a + b represents the stream:
a + b : a0 + b0 a1 + b1 a2 + b2 … an + bn …
Thus, assuming that a and b have the following values:
a : 2 3 5 7 11 13 …
b : 1 1 2 3 5 8 …
Then:
It is important to note that lifting a combinatorial operator (like the example above) to
the stream level does not make it a temporal operator: in each time step the lifted
combinatorial operator has only access to the values in the current time step of its
stream operands. A temporal operator, on the other hand, is free to access the
entire stream of values of its operands. The X operator (read “next operator”) is
an example of a temporal operator which is usually thought of as returning the
“next value” of its stream operand. To be precise however, the X operator returns a
stream which is shifted one step to the left relative to its operand. To continue our
example:
X(a + b) : 4 7 10 16 21 …
In Section 10 the semantics of the HLL nonterminal <expr> is defined using streams (an
<expr> is a stream). Therefore we will use the term stream both for the concept described
above and for any HLL expression <expr>.
In the following sections we will introduce some concepts and aspects of streams, which will be
used to define the semantics of HLL. The most central concept is the (typed) stream model
MT which is just a mapping from a pair (stream of type T, time step) to a value of the type
T, or nil (which is an exceptional value used to model undefined behaviour such as a division
by zero). For example, Mint applied to the stream a of type int above would return the
following values:
Mint(a,0) = 2
Mint(a,1) = 3
Mint(a,2) = 5

2.1.1 Models
Definition 1 (stream model). A Stream Model MT of the set S of HLL stream
expressions (defined in Section 10) of type T is a binary function MT : S×ℕ → T∪{nil},
where ℕ is the set of non-negative integers denoting the time steps of the streams (with
0 representing the initial time step) and nil is an exceptional value defined below.
The precise rules for the computation of the stream models are defined throughout the
document (mainly in Sections 10 and 12). A general rule however, is that any stream
s which has not its value defined in time step k by one of these precise rules, is free to
take any value of its type T in time step k in any model MT, i.e. MT(s,k) ∈ T. This
general rule applies typically to input streams.
Definition 2 (many-sorted model). Letting 𝒯 denote the set of all possible HLL types
(defined in Section 8), both explicit and implicit ones, we will define a Many-Sorted
Model M as the following set: M = {MT | T ∈𝒯}.
2.1.2 Exceptional Value
Definition 3 (nil). A stream s of type T which is not well-defined at time step k in
some model MT takes the exceptional polymorphic value nil in that time step, i.e.
MT(s,k) = nil.
2.1.3 Propositions
Definition 4 (proposition). Given a Boolean stream s, the set of possible Propositions
over s, and their meaning, are:
| Proposition | Meaning | |
| 𝕀 s | s is true in time step 0 | |
| □s | s is always true | |
| | |
2.1.4 Consequences
Definition 5 (consequence). A proposition q is a Consequence of a set of propositions P iff
for all many-sorted models M, the following holds:
where 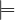 D is a semantic relation between models and propositions defined as:
D is a semantic relation between models and propositions defined as:
-
1.
- M
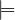 D𝕀 s iff Mbool(s,0) ∈ D for Mbool ∈ M.
D𝕀 s iff Mbool(s,0) ∈ D for Mbool ∈ M.
-
2.
- M
 D□s iff Mbool(s,n) ∈ D for Mbool ∈ M and for all n.
D□s iff Mbool(s,n) ∈ D for Mbool ∈ M and for all n.
The weak variant of 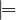 D, written
D, written  w, uses the definition above with D = {true,nil}, and the
strong variant, written
w, uses the definition above with D = {true,nil}, and the
strong variant, written 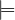 s, uses the definition above with D = {true}. We note
that if the streams underlying the propositions in P ∪{q} are all well-defined in all
time steps of all models, then this distinction in a weak and a strong case becomes
unnecessary.
s, uses the definition above with D = {true}. We note
that if the streams underlying the propositions in P ∪{q} are all well-defined in all
time steps of all models, then this distinction in a weak and a strong case becomes
unnecessary.
(An alternative term for “model” is “scenario” (such as a counterexample), and the formal
definition above simply states that all those, and only those, scenarios (or models) which do
not falsify any of the propositions in P need to satisfy the proposition q in order for the latter
to be a consequence of the former. We can think of the propositions P as the set
of constraints in an HLL text H, and the proposition q as a proof obligation. The
problem of deciding whether q is a consequence of P is known as “model checking”
, and
it amounts to checking the formula (1) above for all models. If there is no counter-model M to
(1), we say that H is a model for q (q is true in H). Admittedly, the use of the word “model”
for different purposes may be confusing, but it has historical reasons, and for the
purposes of this document it is enough to consider a “model” to be synonymous with
“scenario”.)
2.1.5 Static Flag
Definition 6 (static flag). The function 𝒮ℱ : S → {0,1,2} returns the Static Flag
of a stream. A stream s which is Static takes the same value in each time step, i.e.
MT(s,n) = v for some v ∈ T ∪{nil} and for all n. The static flag for each type of stream
expression will be given in association with the semantic description of the expression
(i.e. throughout the document). However, the informal meaning of the values of the
static flag is given in the following table (in order to provide the reader with an intuition
about these values).
| Static Flag | Informal Meaning | |
| 𝒮ℱ(s) = 0 | s is not known to be static | |
| 𝒮ℱ(s) = 1 | s is static | |
| 𝒮ℱ(s) = 2 | s is static and a combination of only constants and literal values | |
| | |
The static flag is used to restrict the set of possible HLL types and stream expressions.
In Section 10.4 we extend the static flag to domains (nonterminal <domain>), which are
streams of sets of values, and in Section 12 we extend it to collections of streams (nonterminal
<collection>).
2.2 Logic of Exceptions
In HLL, many operations such as division by zero, overflow, array indexing out of bounds
et.c., give rise to the exceptional value nil introduced in Section 2.1.2.
This exceptional value, nil, propagates unhindered through most HLL operations, but are
absorbed by a few, such as the if-then-else and the Boolean operations with absorbing values
(and, or, implication). In order to preserve the commutativity of the Boolean operators, they
are defined to be symmetric in the sense that nil can be absorbed on either side of the
operator .
(This means that “true or nil” and “nil or true” both mean “true”.)
We note, however, that any implementation of HLL which lets nil propagate more freely,
and for example reduces “nil or true” to nil instead of “true”, is still safe due
to the fact that nil is accepted by  w on the left hand side of the consequence
relation defined by formula (1) in Section 2.1.4 above, whereas it is rejected by
w on the left hand side of the consequence
relation defined by formula (1) in Section 2.1.4 above, whereas it is rejected by  s on
the right hand side. This asymmetry in the consequence relation ensures that an
implementation which propagates nil more freely will accept more models in the
antecedent and less models in the consequent making it strictly harder to satisfy formula
(1).
s on
the right hand side. This asymmetry in the consequence relation ensures that an
implementation which propagates nil more freely will accept more models in the
antecedent and less models in the consequent making it strictly harder to satisfy formula
(1).
2.3 Namespaces and Scoping
In HLL, names (identifiers) reside in different namespaces depending on which kind of entity
they name. (This means that entities of different kind may have the same name within the
same scope, as explained below.) The different kinds of entities and their corresponding
namespaces are:
-
1.
- streams,
-
2.
- types,
-
3.
- user namespaces, and
-
4.
- struct components.
For each of the first three kinds of entities in the list above, there is a single namespace,
whereas for struct components, there is one namespace per struct type.
A namespace can (at some fixed point in an HLL text) be divided into scopes, which are
stacked downwards one upon the other. A namespace, in this document, is thus
not a single set of names, but rather a collection of sets of names, one for each
scope.
Assume such a scope stack, for example [S1 S2 … Sn] where S1 is the top-level scope and Sn is
the bottom-most scope (the “current” scope), and some element Si with i ∈ [1,n]. We will call
a scope Sj with j < i an Ascendant scope of Si, and we will call a scope Sk with k > i a
Descendant scope of Si. Note that the scopes S1…Si−1 constitute all the ascendant scopes of Si
whereas the scopes Si+1…Sn only constitute a subset of the descendant scopes of Si since
some of these scopes may have other descendant scopes at other points in the HLL
text.
The entities that are Visible (i.e. that can be referenced) in a given scope are those that exist
in that scope or in one above it (an ascendant scope).
Names must be unique
within a given scope of a namespace, i.e. two different entities existing in the same scope of a
namespace cannot have the same name. However, Hiding is allowed (but not encouraged),
meaning that an entity E1 may have the same name as another visible entity E2 that exists in
an ascendant scope (one higher up in the stack). In such a case we say that E1 Hides E2 in all
scopes in which E1 is visible.
It is important not to confuse “namespace” with “user namespace”; the former is the abstract
concept described above, the latter is a concrete concept of HLL which is defined in
Section 5.
Scopes are introduced by language constructs such as user namespaces, lambda
expressions (Section 10.2), case expressions (Section 10.7.9) and quantifier expressions
(Section 10.7.10). The formal descriptions of those constructs define the start and
end points of the scopes they introduce, and the namespaces the scopes operate
on.
Scopes introduced by user namespaces differ slightly from the scopes introduced by the other
aforementioned language constructs, in that the entities inside the former can be referenced
from the outside by using a path identifier (Section 5.1), whereas the entities inside the latter
can be referenced only within the same scope or a descendant one. These referencing rules are
formally defined in Section 5.1.
The namespaces containing struct components are not subdivided into scopes, since
each struct type introduces its own namespace for the components, as formalised in
Section 8.2.2.
2.4 Notation
See Appendix D for a comprehensive list of words, terms and abbreviations used within this
document.
2.4.1 Syntax-Related Notation
The syntax is given using the following grammar notation (similar to EBNF).
- a nonterminal symbol is written <symbol>;
- a nonterminal definition (a production rule) is introduced by ::= with the defined
nonterminal as a left-hand side;
- a terminal symbol is given by a string separated with quotes
("terminal_string");
- the pipe | separates alternative items (<item1> | <item2>);
- square brackets represent the optional items ([<may-be-used>]);
- braces represent 0 or more times repetitions ({<item>});
- braces extended with + represent 1 or more times repetitions ({<item>}+);
- parentheses are used for explicit grouping in grammar expressions.
For the terminals that are described with a regular expression, the right-hand side of the rule
starts with regexp:.
2.4.2 Semantics-Related Notation
We will use (mostly uppercase) letters in This Font to denote variables representing
nonterminals (i.e. syntactic variables). For example, V, T and E are typically used to
represent respectively the nonterminals <id> (Section 4), <type> (Section 8) and
<expr> (Section 10). However, often we simply use the nonterminal itself for the same
purpose.
In a slight abuse of notation (but in an effort to ensure visual coherency), we extend the use of
these symbols to also denote semantic entities in general (even if they do not have a concrete
HLL syntax), for example the letter T is used throughout the document to denote any
type, even one which does not have an explicit HLL syntax (see Section 8.4 for
examples).
In order to have a compact definition of HLL, the semantics of the various language
constructs is often defined by translation to other, more basic or general, language
constructs.
Typically, for a language contruct C1 and a more basic language contruct C2, we will use the
following two relations to relate C1 to C2:
| Relation | Type | Meaning |
| C1 is equivalent to C2 | equivalence relation | Either of C1 and C2 can be used in place |
| | (reflexive, symmetric | of the other, without change of meaning |
| | transitive) | or correctness, anywhere in an HLL text |
| | | in which all subexpressions have been |
| | | explicitly grouped. |
| | | |
| C1 is reducible to C2 | preorder | C2 can be used in place of C1, without |
| | (reflexive, transitive) | change of meaning or correctness, |
| | | anywhere in an HLL text in which all |
| | | subexpressions have been explicitly |
| | | grouped. |
| | |
To avoid redundancy, whenever we say that C1 is equivalent or reducible to C2 this means that
all relevant restrictions that apply to C2 (directly or indirectly), also apply to C1, even if this is
not explicitly said. Furthermore, if C1 and C2 are expressions they will have the same type
even if this is not explicitly said.
As an example, the expression E1 != E2 is defined as equivalent to ~(E1 = E2). This means
that the relevant restriction that says that the operands of = be of “compatible types with a
finite number of scalar components” also applies to operator !=. By contrast, the restriction
that says that the operand of ~ be of type bool is irrelevant, and does not apply to operator
!=.
To be more precise about which restrictions are relevant, one should consider a “language
construct” as being a function from one or more explicitly grouped HLL strings to a
single explicitly grouped HLL string. For example, if we let = denote the function
EQ(<expr>,<expr>) ⇒ (<expr> = <expr>), and ~ the function NOT(<expr>) ⇒ ~<expr>, then
we can define != as being equivalent to the function composition NOT∘EQ (i.e. first apply EQ
then NOT). The restrictions that apply to the domain of definition of != are thus those that
apply to the domain of definition of NOT∘EQ (which is the same as the domain of
EQ).
If a language construct C1 has additional restrictions compared to another construct C2, but
they are otherwise equivalent, we will typically say that C1 is reducible to C2. As
an example, the expression E1 <-> E2 is reducible to E1 = E2 since the type bool
required of the operands of <-> satisfies the restrictions on =, but not the other way
around.
Occasionally, we will use the relation “C1 is equivalent to C2 except for some property P”. This
means, naturally, that the semantics of C1 and C2 is identical except with regards to the
property P (which is of minor importance). This relation will be used whenever neither of C1
and C2 is reducible to the other, but the semantics of the language constructs are still closely
related.
2.5 Document Structure
This document has been structured around the syntax of
HLL .
The syntax, semantics and restrictions for each set of closely related nonterminals of the
language are grouped together whenever possible and the resulting groups are sorted with the
goal of minimizing forward references. Each such group is placed in its own section that may
contain a short introduction with a few examples followed by a formal definition. Please note
that the introduction and examples are only intended as a help to understand the formal
definition.
In the next section we give an example of how such a section may look like.
2.5.1 Language Construct Example
Here we may give a short informal introduction with a few examples as a help for the reader.
Below, in the blue box, follows the formal definition. The labels (ExampleSyntax), (ExampleSemantics) and (ExampleRestriction) can be used for
referencing purposes either within this document or another one. An index of labels can be
found in Appendix D.
Syntax
(ExampleSyntax)
<nonterminal1> ::= <nonterminal2>
| <nonterminal3>
<nonterminal2> ::= "terminal1" <nonterminal4> "terminal2"
Forward References
-
1.
- Here we give references to the definitions of the nonterminals appearing on
the right hand side of a nonterminal definition and defined in a subsequent
section of the document. Note that nonterminals which are defined in a
subsequent subsection of the present section are not listed here.
Semantics
-
1.
- (ExampleSemantics) Here we define the semantics (meaning) of all nonterminals appearing
on the left hand side of a nonterminal definition above. In this case it means
<nonterminal1> and <nonterminal2>.
Restrictions
-
1.
- (ExampleRestriction) Here we list all the cases of HLL strings which are valid syntactically,
but still not part of the language.
Related Notation
-
1.
- Here we will sometimes introduce notation related to the current language
construct, that is to be used elsewhere in the document.
3 Lexical Structure
Characters in an HLL text shall be encoded in ASCII, or any 8-bit extension of it. The
following characters are not allowed in an HLL text:
| Character | | ASCII value |
| ’\0’ | (null character) | 0 |
| | |
The following characters or character sequences may be inserted freely anywhere between
terminals in an HLL text:
| Characters | | ASCII values |
| ’\t’ | (horizontal tab) | 9 |
| ’\n’ | (new line) | 10 |
| ’\r\n’ | (carriage return followed by new line) | 13, 10 |
| ’ ’ | (white space) | 32 |
| | |
Comments and pragmas, defined below, may also be inserted freely between terminals.
3.1 Comments
Informal Description
An HLL text can contain comments of the following forms:
-
1.
- (CommentDoubleSlash) lines containing a "//" (double slash)
are ignored starting from the "//" sequence up to, and including,
the end of the line character "\n" (including "/*" and "*/");
-
2.
- (CommentSlashStar) characters present between "/*" and "*/"
are ignored (including "//"); comments of this kind can be
nested.
The tokens "//", "/*" and "*/" are considered in the order they appear in
the file.
Here are some examples that illustrate this specification:
int a; // this "/*" is not seen as a comment start
/* the one at the beginning of this line is
// The previous "//" on this line does not start a comment. */
int a; /* the present text is inside a comment
/* this one too */
this one also */
3.2 Pragmas
Informal Description
(Pragma) All the characters after an "@" are interpreted as the text
of a pragma up to, and including, the end of the line character "\n".
Pragmas may be used by tools taking HLL as input language. The
semantics of such pragmas is outside the scope of this document.
From the point of view of this document, "@" is equivalent to "//".
4 Identifiers
Syntax
(IdSyntax)
<id> ::= regexp: [a-zA-Z_][a-zA-Z0-9_]*
| regexp: ’[^\n’]+’
| regexp: "[^\n"]+"
Semantics
-
1.
- (Id) An identifier (<id>) identifies a named entity of an HLL text by its
name, where an entity is either either a type, a stream, a struct component
or a user namespace. An identifier may be used either to give an entity
its name (by a declaration or definition), or to refer to an existing named
entity. In a few cases a reference to a nonexisting entity may cause the
entity to exist. This is called implicit declaration by reference.
-
2.
- (IdSignificantChars) Identifiers are case sensitive and all characters
(including quotes) of an identifier are significant.
Restrictions
-
1.
- (ReservedWords) An <id> may not be a reserved word. The reserved words
are listed in Appendix B.
5 User Namespaces
Syntax
(NamespaceSyntax)
<namespace> ::= <id> "{" <HLL> "}"
Forward References
-
1.
- <HLL> is defined in Section 16.
Semantics
-
1.
- (UserNamespace) A User namespace (<namespace>) is a named container
for names of an <HLL> text, meaning that names contained in different user
namespaces will not clash. More precisely, a user namespace N { HLL }
introduces local scopes in the namespaces of streams, types and user
namespaces that start at the { and ends at the }. These local scopes are
called the top-level scopes of the user namespace, and are not to be confused
with the global top-level scopes.
-
2.
- (UserNamespaceName) The <id> defines the name of the namespace and
it resides in the namespace of user namespaces.
-
3.
- (UserNamespaceScattering) Two <namespace> in the same scope and
with the same <id> refers to the same user namespace. This means
that N { HLL1 } … N { HLL2 } (where … represents anything in the text
that may come in between of the two <namespace>) is equivalent to
N { HLL1 HLL2 }.
Restrictions
(empty)
5.1 Path Identifiers
Path identifiers allow referencing named types or streams in any user namespace (all top-level
members of a user namespace are public and can be referenced from the outside). An
example:
Namespaces:
NS1 { Inputs: x;
Outputs: NS2::x; // Refers to x inside NS2
}
NS2 { Inputs: x;
Outputs: NS1::x; // Refers to x inside NS1
}
Outputs:
NS1::x; // Refers to x inside NS1
NS2::x; // Refers to x inside NS2
In this case, if there is no NS1 on the global top-level then the corresponding <path_id> is
invalid.
Syntax
(PathIdSyntax)
<path_id> ::= <relative_path> <id>
| <absolute_path> <id>
<relative_path> ::= { <id> "::" }
<absolute_path> ::= "::" { <id> "::" }
Semantics
-
1.
- (PathId) A <path_id> refers to an entity with name <id> in some
user namespace (or on global top-level) designated by an optional prefix
which is either a Relative path (<relative_path>) or an Absolute path
(<absolute_path>). An empty prefix designates either the user namespace
in which the <path_id> occurs or else the global top-level (if the <path_id>
occurs there).
-
2.
- (PathRelative) A <relative_path> NS1 :: NS2 :: … :: NSn :: designates a user
namespace NSn that is nested inside user namespaces NS1…NSn−1 where NS1 is
selected by applying the following rules in order:
-
(a)
- If the <relative_path> occurs in a user namespace N and N has a
directly nested user namespace NS1, then this NS1 is selected.
-
(b)
- Otherwise, the user namespace NS1 defined on the global top-level is
selected.
-
3.
- (PathAbsolute) An <absolute_path> :: NS1 :: NS2 :: … :: NSn :: designates a user
namespace NSn that is nested inside user namespaces NS1…NSn−1 where NS1 is
defined on the global top-level.
-
4.
- (PathIdLookup) Given a <path_id> [PATH::]ID, the following rules are applied
to lookup the entity E with the name ID:
-
(a)
- If no PATH is given, then the scope stack to consider for the
search is the maximal one ending where the <path_id> occurs, i.e.
[S1 S2 … Sn], where S1 corresponds to the global top-level and Sn
corresponds to the current (bottom- or inner-most) scope.
-
(b)
- If a PATH is given, then the search for ID is made only at the
top-level scope SPATH of the user namespace designated by PATH. The
scope stack to consider for the search is thus [SPATH].
-
(c)
- Given a scope stack [S1 S2 … Sk] as determined from cases 4a and
4b, the search for ID starts in Sk and then proceeds in the order
Sk−1,Sk−2,…S2,S1. The search stops as soon as an entity E with the
name ID is encountered in one of the Si, and it is this entity E which the
<path_id> refers to. The semantics or correctness of a <path_id> that
does not refer to any existing entity E depends on the context in which
the <path_id> is used. The general rule is that such a <path_id> is
incorrect, and the only exception to this rule are unqualified named
expressions, which implicitly declare the nonexisting stream variables
they refer to, causing them to exist (see (NamedExprImplicitDecl) of
Section 10.7.3).
Restrictions
-
1.
- (PathIdNoImplicitDecl) A qualified <path_id> (i.e. a <path_id> with at
least one occurrence of ::) shall refer to an existing entity (no implicit
declaration by reference).
This means that the path identifiers i and N :: i in the lambda expression below do not refer to the same
entity named i, since the first one refers to the lambda parameter and the second one to the input
variable.
| Namespaces : N { | Inputs : | i; |
| | Outputs : | lambda(bool) : (i) := i & N :: i; } |
6 Lists
Lists are a purely syntactic concept that has no particular semantics.
Syntax
<id_list> ::= <id> {"," <id>}
<type_list> ::= <type> {"," <type>}
<expr_list> ::= <expr> {"," <expr>}
Forward References
-
1.
- <type> is defined in Section 8.
-
2.
- <expr> is defined in Section 10.
Semantics
(empty)
Restrictions
(empty)
7 Declarators
Declarators in HLL provide a way to declare objects of array and function type that reflects
the use of the objects. For example:
Inputs:
bool A[4][3]; // A is an array of 4 arrays of 3 bool
Outputs:
A[3][2]; // The last element of A (array-indexing is 0-based)
// (This use of A reflects the declaration of A)
An equivalent notation, shown below, is the array-type notation introduced in Section 8.2.4,
and it is this rewriting from declarators to proper type notation that is performed by the
function calc_type on the next page.
Inputs:
bool^(3)^(4) A; // A is an array of 4 arrays of 3 bool
Outputs:
A[3][2]; // The use of A does not reflect
// the declaration of A anymore
An analogue example can be made using function declarators and function-type notation, for
example the declaration bool f(int) corresponds to the declaration (int -> bool) f using
the function-type notation introduced in Section 8.2.3.
Note that for multidimensional arrays the syntax bool A[4, 3] can be used instead of
bool A[4][3] above (the corresponding array-type notation is then bool^(4, 3)). The two
ways to express multidimensionality are similar but not equivalent. The same is true of
functions: in HLL we can both have a function taking several parameters (called a
multivariate function) or a function returning another function.
Declarators can be used also in type definitions, as shown in the example below, which is an
equivalent formulation of our example above:
Types:
bool T[4][3]; // T is the type bool^(3)^(4)
Inputs:
T A;
Outputs:
A[3][2];
Syntax
(DeclaratorSyntax)
<declarator> ::= <id> {<declarator_suffix>}
<declarator_suffix> ::= "[" <expr_list> "]"
| "(" <type_list> ")"
Semantics
-
1.
- (Declarator) A Declarator (<declarator>) consists of an identifier <id>
and an optional declarator suffix (<declarator_suffix>).
-
2.
- (DeclaratorTypeCalc) The recursive function calc_type defined below takes as
input a base type T (a <type>) and a list of <declarator_suffix> D
and returns an augmented type (which is typically associated with the
identifier <id> of the corresponding <declarator>, if any). Note that the
base type T is not provided from a <declarator>. Instead it typically
comes from an enclosing syntactic rule. See for example <type_def> in
Section 8.
| calc_type(<type> T, {<declarator_suffix>} D) {
let L be the last <declarator_suffix> of D and let D∖L
denote D without L in :
if L is [E1, E2,…En] :
return calc_type(T (E1, E2,…En), D∖L).
else if L is (T1, T2,…Tn) :
return calc_type((T1 ∗T2 ∗…∗Tn -> T), D∖L).
else (D is empty) :
return T.
} | | | | | |
Please note that the array type notation T (E1, E2,…En) is defined in
Section 8.2.4 and the function type notation (T1 ∗T2 ∗…∗Tn -> T) in
Section 8.2.3.
Restrictions
-
1.
- (DeclArrayDimInteger) Each Ei of a declarator suffix [E1, E2,…En] shall be
of integer type (see Section 8.1.2).
-
2.
- (DeclArrayDimConstant) 𝒮ℱ(Ei) = 2 for a declarator suffix [E1, E2,…En].
-
3.
- (DeclFunctionParamScalar) Each Ti of a declarator suffix (T1, T2,…Tn)
shall be scalar (see Section 8.1).
8 Types
Types in HLL should be understood as sets of values. As an example the Boolean type
(written bool) is the set {false,true}. Types are assigned to stream variables (named streams)
either by explicit declaration (see Section 11), by inference (see (DefUndeclaredType) of
Section 12), or in rare cases by reference (see (NamedExprImplicitDecl) of Section 10.7.3).
Types are assigned to stream expressions (unnamed streams) by type inference based on the
operator and the types of operands (if the operator is overloaded to handle more than one
type of operands). The precise typing rules are given in connection with the definition of the
expressions’ semantics (i.e. throughout Section 10).
A stream can only take values of its assigned type (regardless of how the stream was assigned
the type), or the exceptional value nil in response to an exceptional event such as a division
by zero or an overflow.
We will treat nil as a truly exceptional value that does not belong to the types propers.
Syntax
(TypeSyntax)
<type> ::= <bool>
| <integer>
| <tuple>
| <structure>
| <function>
| <array>
| <named_type>
<type_def> ::= <type> <declarator> {"," <declarator>}
| <enum_def>
| <sort_def>
Semantics
-
1.
- (Type) A Type (<type>) is a (possibly empty, possibly infinite) set of
values. For example, the Boolean type bool is the set false,true}.
-
2.
- (TypeDef) <type_def> is a type definition (or a definition of a named type)
that associates an identifier <id> to a type. The identifier can be used, as
part of a <path_id>, wherever a <type> is expected. If a type is defined
using a <declarator>, then it is the first <id> of that <declarator> that
is being defined.
-
3.
- (TypeIdSpace) The identifier of a type resides in the namespace of types,
and is visible everywhere in its scope, regardless of the position of the
<type_def>.
-
4.
- (TypeCalc) The resulting type associated to the identifier being defined
by a type definition (a <type_def>) involving a <type> (the base type)
and a <declarator> is calculated according to procedure calc_type in
Section 7.
-
5.
- (InlineMultTypeDef) A single type definition <type> D1,D2,…Dn where
each Di is a <declarator> is equivalent to n type definitions
<type> D1, <type> D2, …<type> Dn.
-
6.
- (TypeCompatibility) The Compatibility relation C(T1,T2) between types
is an equivalence relation (reflexive, symmetric and transitive) defined in
the remainder of the document. Two types are said to be Compatible iff
C(T1,T2) = true. In Section 10.4 we will extend this relation to include
domains (<domain>).
-
7.
- (TypeAssignability) The Assignability relation A(T1,T2) between types is a
preorder (reflexive and transitive) defined in the remainder of the document.
A type T1 is said to be Assignable to another type T2 iff A(T1,T2) = true.
Restrictions
-
1.
- (TypeDefUnicity) A named type which is defined by a <type_def> which
is not a <sort_def> may only be defined once per scope of the namespace
of types.
-
2.
- (TypeDefCausality) A named type may not be defined in terms of
itself, either directly or indirectly. This restriction also applies to sort
contributions: a sort may not contribute to its own definition.
8.1 Scalar Types
Scalar Types are the subset of HLL types that consists of scalar (or atomic) values. These are
the Boolean, integer, enum and sort types.
8.1.1 Boolean Type
Syntax
(BoolSyntax)
<bool> ::= "bool"
Semantics
-
1.
- (BoolValues) The type bool is comprised of the two values true and false.
-
2.
- (BoolCompatibility) The bool type is compatible with itself.
-
3.
- (BoolAssignability) The bool type is assignable to itself.
-
4.
- (BoolValueOrder) false < true.
Restrictions
(empty)
8.1.2 Integer Types
HLL’s integer types can be either finite or infinite (the set ℤ). Finite types are restricted by
either an inclusive range (for example int [4, 9]), or an “implementation” (for example
int signed 32). Historically, the main purpose of finite integer types has been to give bounds
to inputs (free variables) and state-holding elements (latches and pre-expressions), thus
ensuring that the state-space of an HLL system is finite. However, since HLL version
3.0, all stream variables declared with a finite integer type T will in each time step
only take values from T, except on overflow which will result in nil being taken
instead.
Syntax
(IntSyntax)
<integer> ::= "int"
| "int" <sign>
| "int" <range>
<sign> ::= "signed" <id_or_int>
| "unsigned" <id_or_int>
<id_or_int> ::= <id>
| <int_literal>
<range> ::= "[" <expr> "," <expr> "]"
Forward References
-
1.
- <expr> is defined in Section 10.
Semantics
-
1.
- (IntValues) The type int is comprised of all integers (the set ℤ).
-
2.
- (IntSignedValues) The type int signed E1 is comprised of the integers in
the interval [−2E1−1,2E1−1 −1].
-
3.
- (IntUnsignedValues) The type int unsigned E2 is comprised of the
integers in the interval [0,2E2 −1].
-
4.
- (IdOrInt) <id_or_int> is a constant stream expression restricted to integer
constants (<id>) and integer literals (<int_literal>).
-
5.
- (IntRangeValues) The type int [E3,E4] is comprised of the integers in the
interval [E3,E4].
-
6.
- (IntCompatibility) All integer types are compatible with each other.
-
7.
- (IntAssignability) All integer types are assignable to each other.
-
8.
- (IntValueOrder) i < i + 1 for any integer i.
Restrictions
-
1.
- (IntSizeInteger) E1,E2,E3 and E4 shall be of integer type.
-
2.
- (IntSizeConstant) 𝒮ℱ(Ei) = 2 for i ∈ [1,4].
-
3.
- (SignedBitsPositive) E1 > 0.
-
4.
- (UnsignedBitsNonNegative) E2 ≥ 0.
-
5.
- (IntSizeNotNil) Mint(Ei,k)≠nil for i ∈ [1,4] and all k.
Related Notation
-
1.
- The types int <sign> are called Integer implementation types.
-
2.
- The types int <range> are called Integer range types.
8.1.3 Enum Types
Syntax
(EnumSyntax)
<enum_def> ::= <enumerated> <id>
<enumerated> ::= "enum" "{" <id_list> "}"
Semantics
-
1.
- (EnumDef) The enum type defined as enum {V1,V2,…Vn} is comprised of
the values {V1,V2,…Vn}.
-
2.
- (EnumValueSpace) The values of an enum type reside in the namespace of
streams.
-
3.
- (EnumValueDef) The definition of an enum type also defines its values.
-
4.
- (EnumCompatibility) An enum type is compatible with itself.
-
5.
- (EnumAssignability) An enum type is assignable to itself.
-
6.
- (EnumValueOrder) Vi < Vi+1.
Static Flag
-
1.
- (EnumValueStaticFlag) 𝒮ℱ(V) = 2 for an enum value V.
Restrictions
-
1.
- (EnumValueUnicity) An enum value may not be defined more than once
per scope of the namespace of streams.
8.1.4 Sort Types
Syntax
(SortSyntax)
<sort_def> ::= "sort" [ <sort_contrib> "<" ] <id>
<sort_contrib> ::= <path_id_list>
| "{" <id_list> "}"
<path_id_list> ::= <path_id> {"," <path_id>}
Semantics
-
1.
- (SortDef) A <sort_def> is a contribution to the definition of a sort type.
A <sort_def> without a <sort_contrib> is an empty contribution to the
sort type. (The name of the sort type is given by the <id> as in any type
definition.)
-
2.
- (SortContrib) A sort type is defined by one or more contributions. The
values of the sort type is the union of the values of its contributions.
-
3.
- (SortContribScope) Contributions to a sort type S can only be made within
the same scope.
-
4.
- (SortValueSpace) The values of a sort type reside in the namespace of
streams.
-
5.
- (SortSubTypeContrib) sort S1,S2,…Sk < S denotes the contribution of
sort types S1,S2,…Sk to sort type S, and the inclusion of their values into S
(i.e. S1 ∪S2 ∪…∪Sk ⊆ S).
-
6.
- (SortValueContrib) sort {V1,V2,…Vn} < S denotes the definition of the
values V1,V2,…Vn, and their inclusion into the sort type S (i.e.
{V1,V2,…Vn}⊆ S).
-
7.
- (SortCompatibility) All sort types are compatible with each other.
-
8.
- (SortAssignability) A sort type T1 is assignable to another sort type T2
if either T1 is the same type as T2, or T1 contributes, either directly or
indirectly, to the definition of T2.
-
9.
- (SortValueOrder) Not defined.
Static Flag
-
1.
- (SortValueStaticFlag) 𝒮ℱ(V) = 2 for a sort value V.
Restrictions
-
1.
- (SortValueUnicity) A sort value may not be defined more than once per
scope of the namespace of streams.
-
2.
- (SortSubTypes) Si for i ∈ [1,k] of (SortSubTypeContrib) shall refer to sort
types.
Two different sort types named S are defined in the following example. One is defined on the global
top-level and one within the user namespace N:
Types : sort {V1} < S;
Namespaces : N { Types : sort {V2} < S; }
8.2 Composite Types
Composite Types are the subset of HLL types that are not scalar. A composite type is a
composition of HLL types, with each type of the composition said to be a Component of the
composite type. By extension, a stream of composite type is made up by components,
which are themselves streams. The composite types are tuples, structs, arrays, and
functions.
8.2.1 Tuple Types
A tuple type tuple {bool, int [0, 2]} consists of the 2 ∗ 3 = 6 values in the set
bool×int [0,2], i.e. {(false,0),(false,1),(false,2),(true,0),(true,1),(true,2)}.
Syntax
(TupleSyntax)
<tuple> ::= "tuple" "{" <type_list> "}"
Semantics
-
1.
- (TupleType) A tuple is a composition of ordered unnamed components. The
components are ordered according to the order they appear in the text.
-
2.
- (TupleValues) The type tuple {T1,T2,…Tn} is comprised of the values
in the n-fold Cartesian product of its component types, i.e. the set
T1 ×T2 ×…×Tn.
-
3.
- (TupleCompatibility) Two tuple types are compatible iff they have the same
number of components and the types of those components are pair-wise
compatible.
-
4.
- (TupleAssignability) A tuple type T1 is assignable to another tuple type T2
iff they have the same number of components and each component of T1 is
assignable to its corresponding component in T2.
Restrictions
(empty)
Related Notation
-
1.
- Given a value VT of tuple type tuple {T1,T2,…Tn} and an integer literal
K with 0 ≤ K < n, we will write VT@K to denote the component of VT of
type TK+1 at the 0-based index K. Note that @ is an operation on tuple
values, and distinct from the HLL tuple accessor (.K) that operates on
tuple streams.
8.2.2 Struct Types
From a user’s perspective, the only difference between a struct and a tuple is the way to access
the components: struct components are accessed by their names, whereas tuple components
are accessed using a 0-based integer index. The two types are nevertheless distinct and cannot
be mixed.
Syntax
(StructSyntax)
<structure> ::= "struct" "{" <member_list> "}"
<member_list> ::= <id> ":" <type> {"," <id> ":" <type>}
Semantics
-
1.
- (StructType) A struct is a composition of ordered named components. The
components are ordered according to the order they appear in the text.
-
2.
- (StructValues) The type struct {M1 : T1,M2 : T2,…Mn : Tn} is comprised of
the same values as the corresponding tuple type tuple {T1,T2,…Tn} (see
(TupleValues)).
-
3.
- (StructCompIdSpace) The identifiers of the components reside together in
their own namespace. (One can see this as the struct type introducing a
new namespace to which the named components belong. This means that
two struct types may have components with the same name without any
clash, even if one is nested within the other.)
-
4.
- (StructCompatibility) Two struct types are compatible iff they have the
same number of components and the types of those components are
pair-wise compatible and the names of those components pair-wise equal.
-
5.
- (StructAssignability) A struct type T1 is assignable to another struct type
T2 iff they have the same number of components and each component of T1
has the same name as, and is assignable to, its corresponding component
in T2.
Restrictions
-
1.
- (StructCompUnicity) Two components of the same struct type may not
have the same name.
Related Notation
-
1.
- Given a value VS of struct type struct {M1 : T1,M2 : T2,…Mn : Tn} and an
identifier Mi with 1 ≤ i ≤ n, we will write VS@Mi to denote the component
of VS of type Ti with the name Mi. Note that @ is an operation on struct
values, and distinct from the HLL struct accessor (.M) that operates on
struct streams.
Corresponding means here “at the same position” (the components of struct types are ordered).
8.2.3 Function Types
A function type (int [0, 2] -> bool) consists of the three components (of type bool)
corresponding to the inputs 0, 1 and 2. The type consists of the 23 = 8 values in the set
bool|int[0,2]|, i.e. {(false,false,false), (false,false,true), (false,true,false), (false,true,true),
(true,false,false), (true,false,true), (true,true,false), (true,true,true)}.
This example of a function type adopts the point of view that the function is a composite
object (much like an array) consisting of three components. However, there is also the
alternative point of view of a function as a mapping between two sets; the domain and the
range (or image). Seeing our example above from this point of view, we will identify the
domain with the set {0,1,2} and the range with the set {false,true}. A function value is thus
equivalent to a mapping from a value of the function’s domain to a value of the function’s
range .
For example the function value (false,true,true) from the example above corresponds to the
mapping 0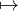 false,1
false,1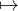 true,2
true,2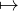 true.
true.
We note that in the “object view” of a function type, the components have to be ordered in a
way that allows us to find the component value corresponding to a given input value, whereas
in the “mapping view” such an order is not needed. Since function values expressed as
n-tuples is a completely abstract concept and not related to any HLL operation, it means that
for the “object view” of function types, any order of the components will work as long
as it is consistently used. That being said, some concrete HLL operations such as
the definition of a function using a collection on the right hand side, written as
f := {false, true, true}; and defined in Section 12, do require that a known order is
defined for the function components. This order is defined by (FunctionCompOrder) on the
next page, and is only defined for ordered domain types (thus excluding functions of sort
domain).
Since a function value is a mapping from a value (of the function’s domain) to a value (of the
function’s range), it would be natural to assume that a stream of function values is a mapping
from a stream to a stream. This is not the case however, and may be a source of confusion. An
HLL function is a stream of combinatorial functions (i.e. mappings from values to values) and
not a function on streams, which means it is not possible to use HLL functions
to express temporal functions (i.e. functions which talk about the past or future
values of their stream parameters). HLL functions are characterized by the following
property:
for each time step k, x = y -> f(x) = f(y), regardless of the history (past or future values)
of x and y.
Expressions such as f(x) (which are introduced in Section 10.6) where both f and x are
streams, should thus be understood as the point-wise application of the value of f on the value
of x in each time step:
f : f0 f1 f2 … fn …
x : x0 x1 x2 … xn …
f(x) : f0(x0) f1(x1) f2(x2) … fn(xn) …
This means that e.g. int [0,7] is considered equal to int unsigned 3.
Syntax
(FunctionSyntax)
<function> ::= "(" <type> {"*" <type>} "->" <type> ")"
Semantics
-
1.
- (FunctionType) A function is a composition of unnamed components, which
are all of the same Return type.
-
2.
- (FunctionValues) A function type (T1 ∗T2 ∗…∗Tn -> T) consists of:
-
(a)
- Parameter types T1 to Tn. The set T1 ×…×Tn is also called the
function’s Domain.
-
(b)
- A return type (or component type) T. The set T is also called the
function’s Range.
The function type is comprised of the values in the Cartesian power T|T1×T2×…×Tn|
(alternatively written as the Cartesian product ∏
i∈T1×T2×…×TnT.)
If n > 1 then the function type is said to be Multivariate.
-
3.
- (FunctionCompOrder) The components of a function are ordered iff the
parameter types are ordered, i.e. iff they each have an order defined on their
values. In that case the order of the components is the same as the order of the
parameter types’ values, where the first parameter type is the most significant
one.
-
4.
- (FunctionDomainEquality) Two function parameter types T1 and T2 are said to
be equal iff they are mutually assignable to each other and their sets of values
are equal, i.e. v ∈ T1 ↔ v ∈ T2.
-
5.
- (FunctionCompatibility) Two function types are compatible iff they have
the same number of parameter types and those are all pair-wise equal
according to (FunctionDomainEquality), and their return types are
compatible.
-
6.
- (FunctionAssignability) A function type (T1 ∗T2…∗Tn -> T) is assignable to
another function type (U1 ∗U2…∗Un -> U) iff Ti is equal to Ui (according to
(FunctionDomainEquality)) for i ∈ [1,n] and T is assignable to U.
Restrictions
-
1.
- (FunctionDomainScalar) The parameter types Ti for i ∈ [1,n] of a function
type (T1 ∗T2 ∗…∗Tn -> T) shall be of scalar type.
Related Notation
-
1.
- Given a value VF of function type (T1 ∗T2 ∗…∗Tn -> T) and values Vi with
Vi ∈ Ti, we will write VF(V1,V2,…Vn)V to denote the component (or output)
value of VF of type T corresponding to the inputs V1,V2,…Vn. We employ
a subscript V on the right parenthesis ()V) in order to emphasize that this
is an operation on function values, and distinct from the HLL function
accessor that operates on function streams. Of course, the subscript V is not
strictly necessary since function values are functions in the mathematical
sense (mappings from values to values) and the operation ()v corresponds
thus to the usual function application in the mathematical sense.
8.2.4 Array Types
An array type bool^(3) (an array of 3 bool) is equivalent to the function type
(int [0, 2] -> bool), except for the way to access the components (A[0] vs
A(0)).
Syntax
(ArraySyntax)
<array> ::= <type> "^" "(" <expr_list> ")"
Semantics
-
1.
- (ArrayType) An array is a composition of ordered unnamed components,
which are all of the same Base type.
-
2.
- (ArrayValues) The type T (E1,E2,…En) is equivalent to the function type
(int [0,E1 −1] ∗int [0,E2 −1] ∗…∗int [0,En −1] -> T), except for the
way to access the components. T is the base type (the component type) of
the array and the Ei are called the Dimensions of the array and if n > 1
then the array type is said to be Multidimensional.
-
3.
- (ArrayCompatibility) An array type T1 (D1,D2,…Dn) is compatible with
another array type T2 (E1,E2,…En) if each Di = Ei and T1 is compatible with
T2.
-
4.
- (ArrayAssignability) An array type T1 (D1,D2,…Dn) is assignable to another
array type T2 (E1,E2,…En) if each Di = Ei and T1 is assignable to T2.
Restrictions
-
1.
- (ArrayDimConstant) 𝒮ℱ(Ei) = 2 for i ∈ [1,n].
-
2.
- (ArrayDimNotNil) Mint(Ei,k)≠nil for i ∈ [1,n] and all k.
Related Notation
-
1.
- Given a value VA of array type T (E1,E2,…En), and values Vi with
0 ≤ Vi < Ei of integer type, we will write VA[V1,V2,…Vn]V to denote the
component of VA of type T at index V1,V2,…Vn. We employ a subscript V on
the right square bracket (]V) in order to emphasize that this is an operation
on array values, and distinct from the HLL array accessor that operates on
array streams.
This means that it is possible to consistently replace all array types by equivalent function types (while
changing all accesses from [i1,…in] to (i1,…in)) in an HLL text. However, array and function types are
still not compatible with or assignable to each other as specified by (ArrayCompatibility) and
(ArrayAssignability).
8.3 Named Types
Syntax
(NamedTypeSyntax)
<named_type> ::= <path_id>
Semantics
-
1.
- (NamedType) A named type (<named_type>) is the type that it refers to.
-
2.
- (NamedTypeCompatibility) A named type is compatible with the type it
refers to.
-
3.
- (NamedTypeAssignability) A named type is mutually assignable with the
type it refers to.
Restrictions
-
1.
- (NamedTypeRef) The <path_id> of a <named_type> shall refer to an
existing type (in the namespace of types).
8.4 Implicit Types
Implicit types have no explicit syntax, but can appear implicitly as a result of some other
syntactic construct of the language. For example a <collection> {false, 0} has a
collection type, and an <ite_expr> if E1 then E2 else E3 has a type which is the union
of the types of E2 and E3.
8.4.1 Collection Types
A collection {false, 0} (a <collection>, defined in Section 12) is assignable to a variable
declared with, for example, type tuple {bool, int} or struct {b: bool, i:int}. A
collection {false, true, false} is assignable to a variable V declared, for example, using
one of the following declarations:
tuple {bool, bool, bool} V; // Tuple of 3 bool
bool V[3]; // Array of 3 bool
bool V(int [1, 3]); // Function with 3 bool outputs
bool V(int [4, 6]); // Same, but different indexing
bool V(ExEnum); // + Types: enum {one, two, three} ExEnum;
Syntax
(empty)
Semantics
-
1.
- (CollectionReason) A collection type is the type associated with collections
(<collection>, see Section 12).
-
2.
- (CollectionType) The type of {R1,R2,…Rn} where Ri is of type Ti is the
collection type {T1,T2,…Tn}, composed of n ordered components. We will
count the collection types among the composite types of HLL.
-
3.
- (CollTupleCompatibility) A collection type T1 is compatible with a tuple
type T2 iff they have the same number of components and each component
of T1 is compatible to its corresponding component in T2.
-
4.
- (CollTupleStructAssignability) A collection type T1 is assignable to a tuple
or struct type T2 iff they have the same number of components and each
component of T1 is assignable to its corresponding component in T2.
-
5.
- (CollArrayAssignability) A collection type T1 is assignable to an array type
T2 (E) iff T1 has E components and each one is assignable to T2.
-
6.
- (CollMultiDimArrayAssignability) A collection type T1 is assignable to
a multidimensional array type T2 (E1,E2,…En) (n > 1) iff T1 has E1
components and each one is assignable to T2 (E2,…En).
-
7.
- (CollFuncAssignability) A collection type T1 is assignable to a function
type (T2 -> T3) iff T2 is an ordered type and T1 has |T2| components and
each one is assignable to T3.
-
8.
- (CollMultiVarFuncAssignability) A collection type T1 is assignable to a
multivariate function type (T2 ∗T3 ∗…∗Tn−1 -> Tn) (n > 3) iff T2 is an
ordered type and T1 has |T2| components and each one is assignable to
(T3 ∗…∗Tn−1 -> Tn).
Restrictions
(empty)
8.4.2 Unsized Types
In HLL, it is possible to restrict the set of values of integer inputs and memories, as well as
other declared stream variables, either by using a “range” (e.g. int [0, 7]) or an
“implementation” (e.g. int unsigned 3). However, for arbitrary integer expressions, the only
type used is int without restriction. The Unsized copy of a type (defined below) is used to
remove its size restriction in certain cases, for example when computing the union type of the
two branches of an if-then-else (see Sections 8.4.3 and 10.1).
Syntax
(empty)
Semantics
-
1.
- (UnsizedInteger) The unsized copy of an integer type T is the type int.
-
2.
- (UnsizedScalar) The unsized copy of a non-integer scalar type T is T.
-
3.
- (UnsizedComposite) The unsized copy of a composite type T is a type T’,
in all respects the same as T, but with each component type replaced by
its unsized copy.
Restrictions
(empty)
To give two examples, the unsized copy of tuple {int signed E1,int [E2,E3]} is tuple {int,int}, and
the unsized copy of (int [E1,E2] -> int [E3,E4]) is (int [E1,E2] -> int).
8.4.3 Union Types
Syntax
(empty)
Semantics
-
1.
- (UnionScalar) The union type of n compatible non-sort scalar types T1…Tn
is the unsized copy of T1.
-
2.
- (UnionSort) The union type of n sort or sort union types T1…Tn (i.e. each
Ti may be either a sort type or another sort union type) is a special “sort
union type” Tu. We will count the sort union type among the scalar types
of HLL.
-
3.
- (UnionComposite) The union type of n compatible composite types T1…Tn,
which are not collection types, is a type Tr, in all respects the same as any
of the Ti, but where each component type of Tr is the union type of the n
corresponding component types of T1…Tn.
-
4.
- (UnionTupleCollection) The union type of a tuple type T1 and a compatible
collection type T2 is a tuple type Tr, in all respects the same as T1, but
where each component type of Tr is the union type of the corresponding
component types of T1 and T2. This union is needed to represent the
type of SELECT expressions where the default value is a collection, see
(QuantSelectType).
-
5.
- (SortUnionCompatibility) A sort union type is compatible with both sort
types and other sort union types.
-
6.
- (SortUnionAssignability) A sort union type Tu of the types T1…Tn is
assignable to a sort type Ts iff each Ti for i ∈ [1,n] is assignable to Ts.
Restrictions
(empty)
Note that this definition relies on a recursion, since the Ti may themselves be sort unions. The recursion is
well-founded since at the base case level we only have sort types.
9 Accessors
Accessors are used to designate components of streams of composite type.
Syntax
(AccessorSyntax)
<accessor> ::= "." <id>
| "." <int_literal>
| "[" <expr_list> "]"
| "(" [<expr_list>] ")"
Forward References
-
1.
- <int_literal> is defined in Section 10.7.2.
Semantics
-
1.
- (AccStruct) .M (an <id>) designates a struct component named M.
-
2.
- (AccTuple) .N (an <int_literal>) designates the (N+1):th component of
a tuple (the indexing is 0-based).
-
3.
- (AccArray) At time step k and relative to an array type T (D1,D2,…Dn),
[E1, E2,…En] designates the array component of type T at the index given by
[Mint(E1,k),Mint(E2,k),…Mint(En,k)]V, or if there is no such component
(the index is out of bounds or nil), it designates nil.
-
4.
- (AccFunction) At time step k and relative to a function type
(T1 ∗T2 ∗…∗Tn -> Tr), (E1, E2,…En) designates the function output of
type Tr corresponding to the inputs (MT1(E1,k),MT2(E2,k),…MTn(En,k))V,
or if there is no such output (some input is out of the function domain or
nil), it designates nil.
Restrictions
-
1.
- (ArrayIndexInteger) Each Ei of an accessor [E1, E2,…En] shall be of integer
type.
-
2.
- (FunctionInputScalar) Each Ei of an accessor (E1, E2,…En) shall be of scalar
type.
10 Expressions
Syntax
(ExprSyntax)
<expr> ::= <ite_expr>
| <lambda_expr>
| <binop_expr>
| <membership_expr>
| <unop_expr>
| <proj_expr>
Semantics
-
1.
- (Expr) An Expression E (an <expr>) is a stream (of values) of some type
T.
-
2.
- (EmptyScalarTypeNil) If some scalar component of T (or T itself) is
an empty scalar type, then the corresponding component of a stream
expression E (or E itself) of type T will carry the value nil in each time
step.
-
3.
- (ExprPrecedence) The precedence of expressions is given below in order from
lowest to highest (same line means same precedence):
-
(a)
- <ite_expr>, <lambda_expr>
-
(b)
- <binop_expr>, <membership_expr>
-
(c)
- <unop_expr>
-
(d)
- <proj_expr>
Restrictions
(empty)
Related Notation
-
1.
- We will write E<V1 := R1,V2 := R2,…Vn := Rn> to denote substitution, i.e.
the process of replacing all free occurrences of the variables V1,V2,…Vn in
the expression E with expressions R1,R2,…Rn.
As an example (x + y = z)<z := 5> is equivalent to x + y = 5. By contrast,
(SOME z : [0,4] (x + y = z))<z := 5> is equivalent to
SOME z : [0,4] (x + y = z) (no substitution performed) since the quantifier
variable z is not free in this case (it is bound by the quantification).
10.1 If-Then-Else Expressions
Syntax
(IteExprSyntax)
<ite_expr> ::= "if" <expr> "then" <expr>
{"elif" <expr> "then" <expr>}
"else" <expr>
Semantics
-
1.
- (Elif) elif is equivalent to else if.
-
2.
- (IfThenElse) In each time step, if E1 then E2 else E3 evaluates to 1)
nil if E1 is nil, 2) E2 if E1 is true and 3) E3, otherwise (E1 is false). The
type T of the expression is the union type of the type T2 of E2 and the type
T3 of E3. Formally:
MT(if E1 then E2 else E3,k) =
Static Flag
-
1.
- (IteExprStaticFlag)
𝒮ℱ(if E1 then E2 else E3) = min(𝒮ℱ(E1),𝒮ℱ(E2),𝒮ℱ(E3)).
Restrictions
-
1.
- (IteCondBool) The type of E1 shall be bool.
-
2.
- (IteBranchesCompatible) The types of E2 and E3 shall be compatible.
10.2 Lambda Expressions
Lambda expressions can be used to build unnamed streams of array or function type. For
example “lambda[3]:[i] := i = 1” is an array of the 3 Boolean constants false (at index 0),
true (at index 1), false (at index 2).
Lambda expressions can, together with a definition, be used to build recursive array or
function definitions. As an example, the Fibonacci numbers are calculated by a recursion
below (all proof obligations are valid).
Declarations:
int fibonacci(int);
Definitions:
fibonacci := lambda(int): (i) := if i <= 2 then 1
else fibonacci(i - 1) +
fibonacci(i - 2);
Proof Obligations:
fibonacci(1) = 1;
fibonacci(2) = 1;
fibonacci(3) = 2;
fibonacci(4) = 3;
fibonacci(5) = 5;
Allowing recursion in this manner provides HLL with a powerful tool, but unfortunately it
also means that it becomes possible to express undecidable problems in HLL, since it is
possible to build recursions that do not terminate. Whether or not a recursion will terminate
depends on the reasoning power of tools implementing HLL, and is thus outside the scope of
this document.
A specificity of lambda expressions is how their type is computed. Two lambda expressions
which at a glance may look as if of different type, may in fact be of the same type.
The type of a lambda expression is computed according to (LambdaType) on the
next page. In the following example, the two lambda expressions that are being
compared are of the same type (the type int (3) (4)), and the proof obligation is
valid.
Proof Obligations:
(lambda[4][3]:[i] := (lambda[3]:[j] := 0)) =
(lambda[4]: [i] := (lambda[3]:[j] := 0)); // Valid PO
Lambda expressions are – just as any HLL function (or array) as discussed in Section 8.2.3 –
streams of combinatorial functions (mappings from values to values). The formal definition of
lambda arrays and functions (in (LambdaArray) and (LambdaFunction) below) defines, for a
given time step k, one such combinatorial function. The combinatorial function takes as inputs
the values V1 to Vn and returns:
-
1.
- The value of the right hand side expression at time step k with the formal
parameters substituted with their corresponding values, if the latter are within the
domain of the array or function, or
-
2.
- nil otherwise.
lambda[1] : [i] := (lambda[1] : [i] := i) is not reducible to lambda[1][1] : [i][i] := i (since the latter
expression is not legal), so the two are not equivalent.
Syntax
(LambdaExprSyntax)
<lambda_expr> ::= "lambda" {<declarator_suffix>}+ ":"
{<formal_param>}+ ":=" <expr>
<formal_param> ::= "[" <id_list> "]"
| "(" <id_list> ")"
Semantics
-
1.
- (LambdaScope) A <lambda_expr> introduces a local scope in the
namespace of streams, called a Lambda scope that starts at the
"lambda" keyword and continues to the end of the expression. Parameters
(<formal_param>) declared within the scope must be unique, but can hide
other variables or parameters above it.
-
2.
- (LambdaType) The type T of a lambda expression lambda DS : FP := E
where E is an expression of type T1 is equal to calc_type(T2,DS),
where the type T2 is calculated by solving the following equation:
T1 = calc_type(T2,DS_suffix) where DS_suffix is the N last elements of
the list DS where N is the difference in length of the list DS and the list FP,
i.e. N = |DS|−|FP|. The function calc_type is defined in Section 7.
Note that if the length of the lists DS and FP is the same (i.e. N = 0), then
DS_suffix = {} (the empty list) and T1 = T2.
-
3.
- (LambdaMultFormalParam) lambda D1…Dn : P1…Pn:= E is reducible to
lambda D1…Dn−1 : P1…Pn−1:= (lambda Dn : Pn:= E).
-
4.
- (LambdaDeclSuffixOverhang) lambda D1…Dn : P1…Pk:= E with n > k is (if
well-typed) equivalent to lambda D1…Dk : P1…Pk:= E.
-
5.
- (LambdaArray) lambda[E1,…En] : [i1,…in]:= E, where E is of type TE, and
ij for j ∈ [1,n] is, by definition, of type int, is an expression of type
TE (E1,…En) such that:
MTE (E1,…En)(lambda[E1,…En] : [i1,…in]:= E,k)[V1,…Vn]V =
(Note that the values V1 to Vn are implicitly converted to constant streams
before they are substituted for the formal parameters i1 to in.)
-
6.
- (LambdaFunction) lambda(T1,…Tn) : (i1,…in):= E, where E is of type TE,
and ij for j ∈ [1,n] is, by definition, of type Tj, is an expression of type
(T1 ∗…∗Tn -> TE) such that:
M(T1∗…∗Tn -> TE)(lambda(T1,…Tn) : (i1,…in):= E,k)(V1,…Vn)V =
(Note that the values V1 to Vn are implicitly converted to constant streams
before they are substituted for the formal parameters i1 to in.)
Static Flag
-
1.
- (LambdaStaticFlag) 𝒮ℱ(<lambda_expr>) = 0.
-
2.
- (FormalParamStaticFlag) 𝒮ℱ(i) = 1 for a lambda parameter i (e.g.
lambda[1] : [i] := <expr>).
Restrictions
-
1.
- (LambdaParamUnicity) Two parameters of a lambda expression may not
have the same name.
-
2.
- (LambdaParamsBound) |DS|≥|FP| (the number of elements of the list DS
shall be greater than or equal to the number of elements of the list FP) for
an expression lambda DS : FP := E.
-
3.
- (LambdaParamsMatch) Each element F (a <formal_param>) of the list
FP in an expression lambda DS : FP := E, where F itself is a list (an
<id_list>), shall contain the same number of elements (of form <id>)
as the element D (a <declarator_suffix> and itself a list; either an
<expr_list> or a <type_list) of the corresponding position in the list DS.
Furthermore, if D is on the form "[" <expr_list> "]" then F
shall be on the form "[" <id_list> "]", and if D is on the form
"(" <type_list> ")" then F shall be on the form "(" <id_list> ")".
-
4.
- (LambdaTypeCheck) There shall be exactly one solution to the equation
T1 = calc_type(T2,DS_suffix) of (LambdaType).
10.3 Binop Expressions
Syntax
(BinopSyntax)
<binop_expr> ::= <expr> <binop> <expr>
<binop> ::= "#" | "&" | "#!" | "->" | "<->"
| ">" | ">=" | "<" | "<="
| "=" | "==" | "!=" | "<>"
| "+" | "-" | "*" | "^" | "<<" | ">>"
| "/" | "/>" | "/<" | "%"
Semantics
-
1.
- (BoolAnd) E1 & E2 (Boolean and) is equivalent to ~(~E1 # ~E2) (De
Morgan’s law).
-
2.
- (BoolXor) E1 #! E2 (Boolean exclusive or) is equivalent to ~(E1 <-> E2).
-
3.
- (BoolImpl) E1 -> E2 (Boolean implication) is equivalent to ~E1 # E2.
-
4.
- (BoolEquiv) E1 <-> E2 (Boolean equivalence) is reducible to E1 = E2.
-
5.
- (IntGt) E1 > E2 (greater than) is equivalent to E2 < E1.
-
6.
- (IntGte) E1 >= E2 (greater than or equal to) is equivalent to ~(E1 < E2).
-
7.
- (IntLte) E1 <= E2 (less than or equal to) is equivalent to E2 >= E1.
-
8.
- (OpNeq) E1 != E2 and E1 <> E2 are both equivalent to ~(E1 = E2).
-
9.
- (OpEqEq) == is equivalent to =.
-
10.
- (IntSub) E1 - E2 (subtraction) is equivalent to E1 + (-E2).
-
11.
- (IntLeftShift) E1 << E2 (left shift) is reducible to E1 * (2 E2).
-
12.
- (IntRightShift) E1 >> E2 (right shift) is reducible to E1 /> (2 E2).
-
13.
- (IntFloorDiv) E1 /> E2 (floor division) represents the biggest integer
smaller than or equal to the rational E1∕E2. Formally, it is equivalent
to:
| if (E1 < 0) = (E2 < 0) # E1 % E2 = 0
then E1 / E2
else E1 / E2 - 1 | | | | | |
-
14.
- (IntCeilDiv) E1 /< E2 (ceiling division) represents the smallest integer
bigger than or equal to the rational E1∕E2. Formally, it is equivalent
to:
| if (E1 < 0) = (E2 < 0) & E1 % E2 != 0
then E1 / E2 + 1
else E1 / E2 | | | | | |
-
15.
- (IntRem) E1 % E2 (remainder) is equivalent to E1 - (E1 / E2) * E2.
Core Constructs:
-
16.
- (BoolOr) E1 # E2 (Boolean or) is a stream of type bool for which
Mbool(E1 # E2,n) = Mbool(E1,n) ∨nilMbool(E2,n) holds. The operator
∨nil is the usual Boolean OR operator extended to three-valued logic
according to the following table:
| | | | |
| | B |
| |
|
|
|
| | false | nil | true |
| | | | |
| | | | |
| | false | false | nil | true |
| | | | |
| A | nil | nil | nil | true |
| | | | |
| | true | true | true | true |
| | | | |
-
17.
- (IntLt) E1 < E2 (less than) is a stream of type bool for which
Mbool(E1 < E2,n) = Mint(E1,n) < nilMint(E2,n) holds. The operator < nil is
the usual “strictly less than” comparison operator defined on integers, and
extended for the nil case according to the following table:
| | | |
| | B |
| |
|
|
| | nil | Y |
| | | |
| | | |
|
A | nil | nil | nil |
|
|
|
|
| | X | nil | X < Y |
| | | |
-
18.
- (IntAdd) E1 + E2 (addition) is a stream of type int for which
Mint(E1 + E2,n) = Mint(E1,n) + nilMint(E2,n) holds. The operator +nil is the
usual integer addition operator extended for the nil case according to the
following table:
| | | |
| | B |
| |
|
|
| | nil | Y |
| | | |
| | | |
|
A | nil | nil | nil |
|
|
|
|
| | X | nil | X + Y |
| | | |
-
19.
- (IntMul) E1 * E2 (multiplication) is a stream of type int for which
Mint(E1 * E2,n) = Mint(E1,n) ∗nilMint(E2,n) holds. The operator ∗nil is the
usual integer multiplication operator extended for the nil case according to the
following table:
| | | |
| | B |
| |
|
|
| | nil | Y |
| | | |
| | | |
|
A | nil | nil | nil |
|
|
|
|
| | X | nil | X ∗ Y |
| | | |
-
20.
- (IntDiv) E1 / E2 (integer division) is a stream of type int for which
Mint(E1 / E2,n) = Mint(E1,n)∕nilMint(E2,n) holds. The operator ∕nil is the
usual integer division operator (this means a truncating division; i.e. division
with the fractional part omitted) extended for the nil case according to the
following table:
| | | | |
| | B |
| |
|
|
|
| | 0 | nil | Y |
| | | | |
| | | | |
|
A | nil | nil | nil | nil |
|
|
|
| |
| | X | nil | nil | X∕Y |
| | | | |
-
21.
- (IntExp) E1 E2 (exponentiation) is a stream of type int for which
Mint(E1 E2,n) = Mint(E1,n) ˆnil Mint(E2,n) holds. The operator ˆnil is
defined in the following table:
| | | | | |
| | | B
| |
|
|
|
|
| | < 0 | 0 | nil | Y |
| | | | | |
| | | | | |
| | 0 | nil | 1 | nil | 0 |
| | | | | |
| A | nil | nil | nil | nil | nil |
| | | | | |
| | X | 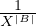 | 1 | nil | XY |
| | | | | |
Note: The division operation 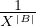 refers to integer division, which means that
this expression can only take the values −1, 0 or 1.
refers to integer division, which means that
this expression can only take the values −1, 0 or 1.
-
22.
- (OpEqScalar) E1 = E2 (scalar equality), where E1 and E2 are of scalar
compatible types T1 and T2, is a stream of type bool for which
Mbool(E1 = E2,n) = (MT1(E1,n) = nilMT2(E2,n)) holds. The operator = nil is
the usual equality operator extended for the nil case according to the following
table:
| | | |
| | B |
| |
|
|
| | nil | Y |
| | | |
| | | |
|
A | nil | nil | nil |
|
|
|
|
| | X | nil | X = Y |
| | | |
-
23.
- (OpEqCompositeUniDim) E1 = E2 (composite unidimensional equality), where
E1 and E2 are of composite compatible types TE1 and TE2, which are neither
multidimensional array types nor multivariate function types, is equivalent
to:
where:
-
24.
- (OpEqCompositeMultiDim) E1 = E2 (composite multidimensional equality),
where E1 and E2 are of composite compatible types TE1 and TE2, which are either
multidimensional array types or multivariate function types, is equivalent
to:
E1A0…00 = E2A0…00 & … & E1A0…0mk = E2A0…0mk &
E1A0…10 = E2A0…10 & … & E1A0…1mk = E2A0…1mk &





E1A0…mk−10 = E2A0…mk−10 & … & E1A0…mk−1mk = E2A0…mk−1mk &





E1Am1m2…0 = E2Am1m2…0 & … & E1Am1m2…mk = E2Am1m2…mk
where:
Ai1…ik =
Precedence and Associativity:
-
25.
- (BinopGrouping) The precedence of the operators is given below in order from
lowest to highest, together with their associativity. Same line means same
precedence.
| Precedence | Associativity | |
| <-> #! | left | |
| -> | right | |
| # | left | |
| & | left | |
| > >= < <= = == != <> | left | |
| << >> | left | |
| + - | left | |
| * / /< /> % | left | |
| ^ | right | |
| | |
Static Flag
-
1.
- (BinopStaticFlag) 𝒮ℱ(E1 <binop> E2) = min(𝒮ℱ(E1),𝒮ℱ(E2)).
Restrictions
-
1.
- (BoolOrEquivOperandsBool) The operands of # <-> shall be of type bool.
-
2.
- (EqOperandsFiniteCompatible) The operands of = shall be either of
compatible scalar types or of compatible composite types with finite
numbers of scalar components (either directly or indirectly via other
composite components).
-
3.
- (IntCoreBinopOperandsInt) The operands of < + * / ^ shall be of integer
type.
-
4.
- (SecondShiftOperandStatic) 𝒮ℱ(E2) ≥ 1 for an expression E1 ∘ E2 with
∘∈{<<, >>}.
-
5.
- (SecondShiftOperandNonNegative) E2 ≥ 0 for an expression E1 ∘ E2
with ∘∈{<<, >>}.
10.4 Membership Expressions
Membership (or elementhood) expressions can be used to test whether the value of
some stream expression belongs to a domain, where a domain is a stream of sets of
values.
Syntax
(MembershipSyntax)
<membership_expr> ::= <expr> ":" <domain>
<domain> ::= <range>
| <type_domain>
<type_domain> ::= <named_type>
| "bool"
| "int"
Semantics
-
1.
- (Domain) A Domain D (<domain>) is a stream of (possibly different) sets
of values. We will write Dk to denote the set of values of D at time step k.
-
2.
- (DomainAsType) A <domain> which is a <type_domain> consists in each
time step of the set of values of the type T which the <type_domain> refers
to. Such a <domain> D is type compatible with the type T.
-
3.
- (DomainAsRange) A <domain> which is a <range> [E1, E2] is in each time
step k the set of values given by the range [Mint(E1,k),Mint(E2,k)]. Such
a <domain> is type compatible with the type int. If either of Mint(E1,k)
or Mint(E2,k) is nil then the <domain> itself is nil at time step k (i.e. we
extend the use of the symbol nil to also include domains).
-
4.
- (Membership) E : D, where E is of type TE, is an expression of type bool
such that:
-
5.
- (MembershipPrecedence) The operator : has the same precedence as the
operator =, and is left-associative.
Static Flag
-
1.
- (MembershipStaticFlag) 𝒮ℱ(<membership_expr>) = 0.
-
2.
- (RangeDomainStaticFlag) 𝒮ℱ([E1, E2]) = min(𝒮ℱ(E1),𝒮ℱ(E2)).
-
3.
- (TypeDomainStaticFlag) The static flag of a <domain> which refers to a
type is 2.
Restrictions
-
1.
- (DomainScalar) A <domain> D shall be type compatible with a scalar type.
-
2.
- (MembershipDomainCompatible) The <domain> D of an expression E : D
shall be type compatible with the type of E.
10.5 Unop Expressions
Syntax
(UnopSyntax)
<unop_expr> ::= <unop> <expr>
<unop> ::= "~" | "-"
Semantics
-
1.
- (BoolNeg) ~E (Boolean negation) is nil, true, or false in time step n if E is
respectively nil, false or true in time step n. The type of the expression is
bool.
-
2.
- (IntNeg) -E (integer negation) is the additive inverse of E (meaning that
E + (-E) = 0 holds). The expression is nil in time step n if E is nil in
time step n. The type of the expression is int.
Static Flag
-
1.
- (UnopStaticFlag) 𝒮ℱ(<unop> E) = 𝒮ℱ(E).
Restrictions
-
1.
- (BoolNegOperandBool) The operand of ~ shall be of type bool.
-
2.
- (IntNegOperandInt) The operand of - shall be of integer type.
10.6 Projection Expressions
Projection expressions can be used to select components of streams of composite
type. For example A[4] selects the array component at index 4, f(true) selects the
function component (or output) that corresponds to input true, and so on. An
important thing to note is that f(x), where x is an arbitrary stream expression,
selects, in time step k, the function output that corresponds to the value of x at time
step k, i.e. M(x,k). This means that functions are characterized by the following
property:
for each time step k, x = y -> f(x) = f(y), regardless of the history (past or future values)
of x and y.
Hence, streams of function type shall be understood as streams of combinatorial functions,
and not as functions on streams.
This is only possible for array and function accessors.
Syntax
(ProjExprSyntax)
<proj_expr> ::= <closed_expr> { <accessor> }
Forward References
-
1.
- <closed_expr> is defined in Section 10.7.
Semantics
-
1.
- (ProjMultipleAcc) A projection expression E A1 A2…An is equivalent to
(…((E A1) A2)…) An.
-
2.
- (Projection) A projection expression E A where E is a <closed_expr> of
composite type T and A an <accessor> compatible with T is equivalent
to the component of E designated by A. If A does not designate a valid
component of E in time step n, then the expression is equivalent to nil in
time step n. Note that the semantics of accessors is detailed in Section 9.
-
3.
- (ProjArrayFunc) This follows directly from Semantic item 4 of Section 9
but is stated again here as a reminder due to its importance:
MT(E(E1,E2,…En),k) = M(T1∗T2∗…∗Tn -> T)(E,k)(MT1(E1,k),MT2(E2,k),…
MTn(En,k))V for all time steps k and types T. (The analogue for array
accessors naturally also holds and follows from Semantic item 3 of
Section 9.)
To clarify what this entails, then as an example, assume for simplicity that n = 1
and the type of E1 is comprised of the values in the set {V1, V2,…Vn}. Then the
expression E(E1) is equivalent to:
| if E1=V1 then E(V1) else
if E1=V2 then E(V2) else
 if E1=Vn−1 then E(Vn−1) else E(Vn)
if E1=Vn−1 then E(Vn−1) else E(Vn) | | | | | |
-
4.
- (ProjExprNil) A projection expression E A where E is nil in time step n is also
nil in time step n.
Static Flag
-
1.
- (ProjExprStaticFlag) 𝒮ℱ(<proj_expr>) = 0.
Restrictions
-
1.
- (ProjAccCompatible) The accessor A of an expression E A must be compatible
with the type T of the expression E, according to the following table:
| |
| A | Compatible type T |
| |
| |
| .K (an <int_literal>) | Tuple with > K components |
| |
| .M (an <id>) | Struct with a component named M |
| |
| [E1, E2,…En] | Array with n dimensions |
| |
| (E1, E2,…En) | Function (T1 ∗T2 ∗…∗Tn -> T) where |
| | the type of Ei is assignable to Ti |
| |
To concretise the example, assume that E is defined with E(i) := ~i & X(i);, then we can use this
equivalence to see that E(input) = (if input = true then E(true) else E(false)) = false, and not
~input & X(input).
10.7 Closed Expressions
Closed expressions are a purely syntactic concept, and consist of the explicitly grouped
expressions.
Syntax
(ClosedExprSyntax)
<closed_expr> ::= <bool_literal>
| <int_literal>
| <named_expr>
| <next_expr>
| <pre_expr>
| <fun_expr>
| <cast_expr>
| <with_expr>
| <case_expr>
| <quantif_expr>
| "(" <expr> ")"
Semantics
-
1.
- (GroupedExpr) M((E),n) = M(E,n) for any model M and time step n.
(E) has the same type as E. Explicit grouping can be used to override
the implicit grouping performed by the parsing of an <expr>. For example
(a + b) * c is not equivalent to a + b * c since operator * has a higher
precedence than operator +.
Static Flag
-
1.
- (GroupedExprStaticFlag) 𝒮ℱ((E)) = 𝒮ℱ(E).
Restrictions
(empty)
10.7.1 Boolean Literals
Syntax
(BoolLitSyntax)
<bool_literal> ::= <true> | <false>
<true> ::= "true" | "TRUE" | "True"
<false> ::= "false" | "FALSE" | "False"
Semantics
-
1.
- (BoolLitTrue) <true> is a
stream of type bool such that Mbool(<true>,n) = true for all time steps
n.
-
2.
- (BoolLitFalse) <false>
is a stream of type bool such that Mbool(<false>,n) = false for all time
steps n.
Static Flag
-
1.
- (BoolLitStaticFlag) 𝒮ℱ(<bool_literal>) = 2.
Restrictions
(empty)
10.7.2 Integer Literals
Syntax
(IntLitSyntax)
<dec_literal> ::= [0-9](_?[0-9])*
<bin_literal> ::= 0[Bb][0-1][_?[0-1])*
<hex_literal> ::= 0[Xx][0-9A-Fa-f](_?[0-9A-Fa-f])*
<int_literal> ::= <dec_literal>
| <hex_literal>
| <bin_literal>
Semantics
-
1.
- (IntLitUnderscores) Underscores (_) may be put freely inside integer literals
with the purpose of improving readability (for example 1_000_000 or
0xFFFF_FFFF). They can be removed completely without changing the
meaning of the literals they appear in, and will not be considered in the
following.
-
2.
- (IntLitDecimal) A <dec_literal> shall be intepreted as an integer in base
10 in the standard way (most significant digit first and least significant digit
last).
-
3.
- (IntLitBinary) A <bin_literal> starts with the prefix 0B or 0b and is
followed by the significant bits. The significant bits shall be interpreted as
an unsigned integer in base 2 in the standard way (MSB first and LSB
last).
-
4.
- (IntLitHexadecimal) A <hex_literal> starts with the prefix 0X or 0x
and is followed by the significant digits. The significant digits shall be
interpreted as an unsigned integer in base 16 in the standard way (most
significant digit first and least significant digit last).
-
5.
- (IntLiteral) An integer literal <int_literal> with the interpreted
value K, as specified above, is a stream of type int such that
Mint(<int_literal>,n) = K for all time steps n.
Static Flag
-
1.
- (IntLitStaticFlag) 𝒮ℱ(<int_literal>) = 2.
Restrictions
(empty)
10.7.3 Named Expressions
Named expressions are references to stream variables.
Syntax
(NamedExprSyntax)
<named_expr> ::= <path_id>
Semantics
-
1.
- (NamedExpr) If the <path_id> of a <named_expr> refers to an existing
stream (in the namespace of streams), then the <named_expr> is that
stream.
-
2.
- (NamedExprImplicitDecl) Otherwise, the <named_expr> (which must be
unqualified as according to (PathIdNoImplicitDecl)) refers to a unique
implicit input stream of type bool. The input stream is implicitly declared
by the <named_expr>. The declaration is made in the top-level scope (of the
namespace of streams) of the user namespace in which the <named_expr>
occurs, or else on the global top-level (if the <named_expr> does not occur
inside a user namespace).
Static Flag
-
1.
- (NamedExprStaticFlag) The static flag of a <named_expr> is equal to the
static flag of the stream it refers to.
-
2.
- (NamedExprUndefinedStaticFlag) The static flag of an undefined stream
variable is 0.
Restrictions
(empty)
10.7.4 Next Expressions
Syntax
(NextExprSyntax)
<next_expr> ::= "X" "(" <expr> ")"
Semantics
-
1.
- (NextExpr) M(X(E),n) = M(E,n + 1) for any model M and time step n.
X(E) has the same type as E.
Static Flag
-
1.
- (NextExprStaticFlag) 𝒮ℱ(<next_expr>) = 0.
Restrictions
(empty)
10.7.5 Pre Expressions
Syntax
(PreExprSyntax)
<pre_expr> ::= ("pre" | "PRE") ["<" <type> ">"]
"(" <expr> ["," <expr>] ")"
Semantics
-
1.
- (PreUppercase) PRE is equivalent to pre.
-
2.
- (PreTypedWithInit) pre<T>(E1,E2) is an initialized memory stream of type
T, where E2 is the initial value for the initial time step and E1 is the
memorized value for all other time steps. Formally, if T1 and T2 correspond
respectively to the types of the expressions E1 and E2, then the value of the
expression at time step k is defined as follows:
-
3.
- (PreTyped) pre<T>(E) is an uninitialized memory stream of type T which
takes the value nil in the initial time step. Formally, if T1 corresponds to
the type of the expression E, then the value of the expression at time step
k is defined as follows:
-
4.
- (PreUntyped) pre(E) is equivalent to pre<T>(E) where T is the unsized
copy (see 8.4.2) of the type of E.
-
5.
- (PreUntypedWithInit) pre(E1, E2) is equivalent to pre<T>(E1, E2) where
T is the union type (see 8.4.3) of the types of E1 and E2.
Static Flag
-
1.
- (PreExprStaticFlag) 𝒮ℱ(<pre_expr>) = 0.
Restrictions
-
1.
- (PreOperandsAssignable) The types of the operands E1 and E2 of pre<T>
(E1,E2) and the type of the operand E of pre<T>(E), shall be assignable to
T.
10.7.6 Function-Style Expressions
Syntax
(FunopSyntax)
<fun_expr> ::= <fop> "(" <expr_list> ")"
<fop> ::= "$min"
| "$max"
| "$abs"
| "$or"
| "$and"
| "$xor"
| "$not"
| "bin2u"
| "u2bin"
| "bin2s"
| "s2bin"
| "population_count_lt"
| "population_count_gt"
| "population_count_eq"
Semantics
-
1.
- (IntMin) $min(E1, E2) (minimum) is equivalent to:
(if E1 < E2 then E1 else E2).
-
2.
- (IntMax) $max(E1, E2) (maximum) is equivalent to:
(if E1 > E2 then E1 else E2).
-
3.
- (IntAbs) $abs(E) (absolute value) is equivalent to:
(if E < 0 then -E else E).
-
4.
- (OpBin2u) bin2u(E1, E2) interprets the E2 first bits of an array E1 of bool
as an unsigned binary number and is equivalent to:
SUM i : [0, E2-1] (2 i * (if E1[i] then 1 else 0)) for a fresh i.
-
5.
- (OpBin2s) bin2s(E1, E2) interprets the E2 first bits of an array E1 of bool
as a signed binary number encoded in the two’s complement notation and
is equivalent to:
-(if E1[E2-1] then 1 else 0) * 2 (E2-1) + bin2u(E1, E2-1).
-
6.
- (OpU2bin) u2bin(E1, E2) converts an integer E1 into an array of type bool (E2)
and is equivalent to:
(lambda[E2] : [i] := bit_is_one(E1, i))
for a fresh i, together with the following declaration and definition (we do not
use bitwise and (operator $and) in the definition of bit_is_one since that
operator is defined in terms of u2bin):
Declarations:
bool bit_is_one(int, int);
Definitions:
bit_is_one(E, i) := ((E >> i) - ((E >> (i + 1)) << 1)) == 1;
-
7.
- (OpS2bin) s2bin(E1, E2) is equivalent to u2bin(E1, E2).
-
8.
- (OpPopCountLt) population_count_lt(E1, E2,…En,K) of n Boolean streams Ei
and an integer stream K is true exactly when less than K of the Boolean streams
are true. The expression is reducible to:
| ((if E1 then 1 else 0) +
(if E2 then 1 else 0) +
 (if En then 1 else 0)) < K
(if En then 1 else 0)) < K | | | | | |
-
9.
- (OpPopCountGt) population_count_gt(E1, E2,…En, K) is equivalent to
~population_count_lt(E1, E2,…En, K + 1).
-
10.
- (OpPopCountEq) population_count_eq(E1, E2,…En, K) is equivalent to
~population_count_lt(E1, E2,…En, K) &
~population_count_gt(E1, E2,…En, K)
-
11.
- (OpBitwiseOr) $or(E1, E2) (bitwise or) is nil in time step k if either of E1
or E2 is nil in time step k. Otherwise the expression is equivalent to
bin2s((lambda[C] : [i] := s2bin(E1, C)[i] # s2bin(E2, C)[i]), C)
for a fresh i and a constant C. C must be big enough to represent all significant
bits of E1 and E2, i.e.
where ub(E) and lb(E) denote, respectively, the maximum and minimum values
the integer expression E may take in any model.
-
12.
- (OpBitwiseXor) $xor(E1, E2) (bitwise xor) is equivalent to
bin2s((lambda[C] : [i] := s2bin(E1, C)[i] #! s2bin(E2, C)[i]), C)
for a fresh i and a constant C. C must be big enough to represent all significant
bits of E1 and E2, i.e.
where ub(E) and lb(E) denote, respectively, the maximum and minimum values
the integer expression E may take in any model.
-
13.
- (OpBitwiseNot) $not(E) (bitwise not) is equivalent to
bin2s((lambda[C] : [i] := ~s2bin(E, C)[i]), C)
for a fresh i and a constant C. C must be big enough to represent all significant
bits of E, i.e.
where ub(E) and lb(E) denote, respectively, the maximum and minimum values
the integer expression E may take in any model.
-
14.
- (OpBitwiseAnd) $and(E1, E2) (bitwise and) is equivalent to
$not($or($not(E1), $not(E2))).
Static Flag
-
1.
- (FunopUnaryStaticFlag) 𝒮ℱ(∘(E1)) = 𝒮ℱ(E1) for ∘∈{$abs, $not}.
-
2.
- (FunopBinaryStaticFlag) 𝒮ℱ(∘(E1, E2)) = min(𝒮ℱ(E1),𝒮ℱ(E2)) for
∘∈{$min, $max, $and, $xor, $or}.
-
3.
- (FunopNaryStaticFlag) 𝒮ℱ(∘(E1,…En)) = 0 for ∘∈{bin2u, bin2s,
u2bin, s2bin, population_count_lt, population_count_gt,
population_count_eq}.
Restrictions
-
1.
- (FunopUnaryCard) The cardinality of the <expr_list> shall be 1 for the
following operators: $abs, $not.
-
2.
- (FunopBinaryCard) The cardinality of the <expr_list> shall be 2 for the
following operators:
$min, $max, bin2u, bin2s, u2bin, s2bin, $and, $xor, $or.
-
3.
- (PopCountNumberStatic) 𝒮ℱ(K) ≥ 1 for an expression ∘(E1,…En, K) with
∘∈{population_count_lt, population_count_gt, population_count_eq}.
10.7.7 Cast Expressions
Syntax
(CastExprSyntax)
<cast_expr> ::= "cast" "<" <type> ">" "(" <expr> ")"
Semantics
-
1.
- (CastExpr) A Cast expression cast<T>(E), of type int, is an (unchecked)
conversion of an integer expression E into the target type T.
-
2.
- (CastSigned) cast<int signed C>(E) is equivalent to:
bin2s(s2bin(E, C), C).
-
3.
- (CastUnsigned) cast<int unsigned C>(E) is equivalent to:
bin2u(s2bin(E, C), C).
-
4.
- (CastNamedType) cast<T>(E) where T is a named type defined, directly
or indirectly, as the type int S (where S is on the form <sign>, see
Section 8.1.2) is equivalent to cast<int S>(E).
Static Flag
-
1.
- (CastStaticFlag) 𝒮ℱ(<cast_expr>) = 0.
Restrictions
-
1.
- (CastTargetIntImpl) The target type of a cast shall be an integer
implementation type, or a named type that is defined, directly or indirectly,
as an integer implementation type.
10.7.8 With Expressions
With expressions can be understood as an operation that creates a modified copy of a
composite stream, where a single component has been arbitrarily modified. For
example “(A with [0] := ~A[0])” is equivalent to the Boolean array A for all
components except the one at index 0, which has been negated. With expressions are
particularly useful when translating assignments of an imperative language into
HLL.
With expressions can be written with collections on the right hand side (see the definition of
<rhs> in Section 12). In order to explain the semantics of with expressions with
collections on the right hand side, we expand them into a chain of with expressions,
each with a single element of the collection on the right hand side (this expansion
would have to be repeated if such an element is in turn another collection). For
example: “(A with [0] := {1, 2, 3})” is expanded, assuming the projection
expression A[0] is of array type (i.e. A is an array of arrays), into the equivalent formula
“(((A with [0][0] := 1) with [0][1] := 2) with [0][2] := 3)”. This expansion is
formalised in (WithCollectionRhsUniDim) below.
The multidimensional case, e.g. when A[0] is a multidimensional array (or multivariate
function), is a bit trickier and formalised in (WithCollectionRhsMultiDim) below. However,
the basic idea is the same.
Syntax
(WithExprSyntax)
<with_expr> ::= "(" <expr> "with" {<accessor>}+ ":=" <rhs> ")"
Forward References
-
1.
- <rhs> is defined in Section 12.
Semantics
-
1.
- (WithCollectionRhsUniDim) (E with A := {R0,R1,…Rn−1}) where E A is
of type TEA, which is neither a multidimensional array type nor a
multivariate function type, is equivalent to:
(…((E with A A0 := R0) with A A1 := R1)… with A An−1 := Rn−1)
where:
-
2.
- (WithCollectionRhsMultiDim) (E with A := {R0,R1,…Rm1}) where E A is
of type TEA, which is either a multidimensional array type or a multivariate
function type, is equivalent to:
(… (…((E with A A0…00 := R0…00) … with A A0…0mk := R0…0mk)
with A A0…10 := R0…10) … with A A0…1mk := R0…1mk)





with A A0…mk−10 := R0…mk−10) … with A A0…mk−1mk := R0…mk−1mk)





with A Am1m2…0 := Rm1m2…0) … with A Am1m2…mk := Rm1m2…mk)
where:
Ai1…ik =
and Ri1…ik are constructed inductively:
(base) Ri1 for i1 ∈ [0,m1] are given above (as the elements of the collection).
(step) Ri1…ij =
-
3.
- (WithMultipleAcc) (E1 with A1 A2…An := E2) is equivalent to
(E1 with A1 A2…An−1 := (E1 A1 A2…An−1 with An := E2)).
-
4.
- (WithArrayAcc) (E1 with [E3, E4,…En] := E2) where E1 is of type
T (C3, C4,…Cn) is equivalent to:
(lambda[C3, C4,…Cn] : [i3, i4,…in] :=
if i3 = E3 & i4 = E4 &…& in = En then E2 else E1[i3, i4,…in])
where ij with 3 ≤ j ≤ n are fresh variables.
-
5.
- (WithFunctionAcc) (E1 with (E3, E4,…En) := E2) where E1 is of type
(T3 ∗T4 ∗…∗Tn -> T) is equivalent to:
(lambda(T3, T4,…Tn) : (i3, i4,…in) :=
if i3 = E3 & i4 = E4 &…& in = En then E2 else E1(i3, i4,…in))
where ij with 3 ≤ j ≤ n are fresh variables.
-
6.
- (WithTupleStructAcc) (E1 with .M := E2) where E1 is of tuple or struct
type T, and E2 is of type TM is identical to E1 for all components except
the one designated by M, which is equal to E2. A formal definition uses the
following equation (with an overloading of operator @):
Static Flag
-
1.
- (WithExprStaticFlag) 𝒮ℱ(<with_expr>) = 0.
Restrictions
-
1.
- (WithAccCompatible) The accessor A in the expression (E with A := R)
must be a compatible accessor w.r.t. the type of E, meaning that the
projection expression E A must be a valid expression.
-
2.
- (WithRhsAssignable) The type of the <rhs> R of an expression
(E with A := R) shall be assignable to the type of the projection
expression E A.
10.7.9 Case Expressions
Syntax
(CaseExprSyntax)
<case_expr> ::= "(" <expr_list> {<case_item>}+ ")"
<case_item> ::= "|" <pattern_list> "=>" <expr>
<pattern> ::= <expr>
| <named_type> ( <id> | "_" )
| "_"
<pattern_list> ::= <pattern> { "," <pattern> }
Semantics
-
1.
- (CaseExpr) In each time step, a case expression
| (E1, E2, … En
|P11, P12, … P1n => R1
|P21, P22, … P2n => R2
   |Pm1, Pm2, … Pmn => Rm)
|Pm1, Pm2, … Pmn => Rm) | | | | | |
evaluates to the first branch Ri for which all the <pattern> items Pi1 to Pin
match the switch expressions E1 to En. Each Pij is matched against, and only
against, the corresponding Ej. The type of the expression is the union of the
types of the Ri.
-
2.
- (CasePatternExpr) A <pattern> item Ep which is an <expr> matches a switch
expression Es in time step k iff Mbool(Ep = Es,k) = true.
-
3.
- (CasePatternType) A <pattern> item T x which is a <named_type> (followed by
either an identifier or a wildcard) matches a switch expression Es in time step k
iff Mbool(Es : T,k) = true.
-
4.
- (CasePatternWildcard) The <pattern> item _ (a wildcard) matches any switch
expression Es (in any time step).
-
5.
- (CaseCapturingVariable) Each <case_item> of a case expression opens a local
scope in the namespace of streams, called a Branch scope, that starts at the =>
and continues to the end of the <case_item>. Given a <pattern> Pij on
the form <named_type> <id> of the <case_item>, the identifier <id>
resides in the branch scope, and if the <case_item> is a match in time
step k, the <id> refers to a local static stream x of type T (similar to a
lambda parameter of Section 10.2), called a Capturing variable, whose
value in each time step is equal to MT(Ej,k), i.e. MT(x,n) = MTE
j(Ej,k)
for all time steps n. In other words, the capturing variable x refers
to a different static stream in each matching time step, and applying
a temporal operator such as X or PRE to such a variable has thus no
effect.
-
6.
- (CaseExprNil) A case expression propagates nil in a similar manner to an
equivalent sequence of if-then-else expressions (see Section 10.1). Furthermore, a
case expression evaluates to nil in a time step k if there is no <pattern_list>
matching the switch expressions in that time step (the case expression is not
exhaustive). In order to formalize this, we will first define the binary function
“match”, with signature match : <expr_list>×<pattern_list> → <expr>, as
follows:
match({E1,…En},{P1,…Pn}) =
Now, given the case expression of (CaseExpr) above, it will evaluate to nil in
time step k if one of the following conditions is true:
-
(a)
- There is no matching <pattern_list> Pi1,…Pin, i.e. one for which
Mbool(match({E1,…En}, {Pi1…Pin}),k) = true, or
-
(b)
- There is a <pattern_list> Pj1,…Pjn above the first matching
<pattern_list> Pi1,…Pin (i.e. with j < i) such that Mbool(match(
{E1,…En}, {Pj1…Pjn}),k) = nil.
(Note that the case expression will of course also evaluate to nil in time
step k in case the matching branch Ri evaluates to nil in time step
k.)
Static Flag
-
1.
- (CaseExprStaticFlag) 𝒮ℱ(<case_expr>) = 0.
-
2.
- (CaseCapturingVarStaticFlag) 𝒮ℱ(x) = 1 for a capturing variable x
corresponding to the <id> of a <pattern> on the form <named_type> <id>.
Restrictions
-
1.
- (CaseSwitchesScalar) The switches in the <expr_list> of a case expression
shall be of scalar type.
-
2.
- (CasePatternsCompatible) The number of pattern items (<pattern>) in
each <case_item> shall match the number of switches in the <expr_list>,
and their types shall be pair-wise compatible, except for wildcards (_).
-
3.
- (CaseBranchesCompatible) The types of the branches (Ri) shall be
compatible.
-
4.
- (CasePatternExprConstant) 𝒮ℱ(E) = 2 for a <pattern> E which is an
<expr>.
-
5.
- (CasePatternTypeSort) A pattern item <pattern> which is a <named_type>
shall refer to a valid sort type.
-
6.
- (CaseCapturingVarUnicity) Two capturing variables of the same branch
may not have the same name.
10.7.10 Quantifier Expressions
Quantifiers in HLL usually operate on static domains (sets of values – much like types) to
create properties over populations of streams. For example, if we have an array
A of 3 integers, declared as int A[3], with the components taking the following
values:
A[0] : 0, 1, 2, 3, ...
A[1] : 0, 0, nil, 1, ...
A[2] : 0, 4, 4, 3, ...
Then the following HLL quantifiers over A take the following values:
ALL i:[0,2] (A[i] < 4): true, false, false, true, ...
SOME i:[0,2] (A[i] = 0): true, true, nil, false, ...
SUM i:[0,2] (A[i]) : 0, 5, nil, 7, ...
PROD i:[0,2] (A[i]) : 0, 0, nil, 9, ...
$min i:[0,2] (A[i]) : 0, 0, nil, 1, ...
$max i:[0,2] (A[i]) : 0, 4, nil, 3, ...
The SELECT operator selects the unique value from the domain that satisfies the given
predicate. If zero or two (or more) values from the domain satisfy the predicate, then nil is
selected instead:
SELECT i:[0,2] (A[i] = 1): nil, 0, nil, 1, ...
Quantification is extended to several domains in the natural way. For example:
ALL i:[0,2], j:[0,2] (i=j # A[i] != A[j]): false, true, nil, false, ...
Quantifiers can also be nested, and the domains of nested quantifiers may depend on the
quantifier variables of the enclosing ones. So the previous formulation could be optimized to
reduce the number of iterations:
ALL i:[0,2] ALL j:[0, i-1] (A[i] != A[j]): false, true, nil, false, ...
Quantification was extended in HLL version 3.0 to allow quantification over (the components
of) array and function streams, using the new operator $items. As an example,
ALL a:$items(A) (a < 4) is equivalent to ALL i:[0,2] (A[i] < 4) above. As two
components of an array or function may be equal, this corresponds to quantification over a
domain which is a multiset of streams (of values). To fit easier with the historical
quantifiers in the formal definition below, we will use an alternative (but equivalent) point of
view and instead define the domain as a stream of multisets (of values). To connect this
with our running example, it means that the domain $items(A) corresponds to the following
stream of multisets:
$items(A): {0, 0, 0}, {1, 0, 4}, {2, nil, 4}, {3, 1, 3}, ...
The use of multisets instead of sets is important only when considering the SUM and PROD
quantifers. For example:
SUM a:$items(A) (1) : 3, 3, 3, 3, ...
Note that the SELECT operator is not allowed in the combination with a domain on the form
$items(A).
This means that upper bound i of the domain of j in the expression ALL i : [0, 10], j : [0, i] (i >= j)
does not refer to the quantifier variable i introduced just before j. On the other hand, in the expression
ALL i : [0, 10] ALL j : [0, i] (i >= j), the upper bound of j does refer to the quantifier variable i in the
enclosing quantifier expression.
Syntax
(QuantExprSyntax)
<quantif_expr> ::= <quantifier> <quantif_vars>
( "(" <expr> ")" | <quantif_expr> )
| "SELECT" <quantif_vars>
( "(" <expr> ["," <rhs>] ")" |
<quantif_expr> )
<quantif_vars> ::= <quantif_var> {"," <quantif_var>}
<quantif_var> ::= <id> ":" <quantif_domain>
<quantif_domain> ::= <domain>
| "$items" "(" <expr> ")"
<quantifier> ::= "SOME" | "ALL" | "SUM" | "PROD"
| "CONJ" | "DISJ" | "$min" | "$max"
Semantics
-
1.
- (QuantScope) A Quantifier expression (<quantif_expr>) introduces a
local scope in the namespace of streams, called a Quantifier scope that
starts right after the last <quantif_var> and continues to the end of the
expression. The quantifier variables (<quantif_var>) exist, and only exist,
within this scope.
-
2.
- (QuantDomainDomain) A quantifier domain D which is a <domain>
corresponds for each time step k to the set of values Dk (see Section 10.4).
Due to restriction (QuantDomainStatic), such a quantifier domain is
guaranteed to be static and not to change from one time step to another.
-
3.
- (QuantDomainItems) A quantifer domain $items(E) where E is of array
or function type TE with component type T corresponds for each time step
k to the following multiset of values:
{MT(E A0…00,k), MT(E A0…01,k), … MT(E A0…0mn,k),
MT(E A0…10,k), MT(E A0…11,k), … MT(E A0…1mn,k),




MT(E A0…mn−10,k),MT(E A0…mn−11,k), … MT(E A0…mn−1mn,k),




MT(E Am1m2…0,k), MT(E Am1m2…1,k), … MT(E Am1m2…mn,k) }
where:
Ai1…in =
-
4.
- (QuantVarType) The type of a quantifer variable i : D is:
-
(a)
- The type compatible with D if D is a <domain>, as according to
(DomainAsType) and (DomainAsRange).
-
(b)
- The component type of the array or function type of E, if D is on the
form $items(E).
-
5.
- (QuantMultVar) QTF i1 : D1, i2 : D2,…in : Dn (E), where QTF is a <quantifier>
other than SELECT and the ii : Di are <quantif_var>, is reducible to
QTF j1 : D1 (QTF j2 : D2 … (QTF jn : Dn (E<i1 := j1,i2 := j2, …in := jn>)) …)
where j1 to jn are fresh identifiers.
-
6.
- (QuantDisj) DISJ is equivalent to SOME.
-
7.
- (QuantConj) CONJ is equivalent to ALL.
-
8.
- (QuantSome) SOME i:D (E), of type bool, evaluates to true in time step k iff
there exists some value j in D such that E, with all occurrences of i replaced by
j, evaluates to true. Formally:
(Where the cases on the right hand side should be considered in order from top
to bottom.)
-
9.
- (QuantAll) ALL i:D (E), of type bool, evaluates to true in time step k iff for all
values j in D, E, with all occurrences of i replaced by j, evaluates to true.
Formally:
(Where the cases on the right hand side should be considered in order from top
to bottom.)
-
10.
- (QuantSum) SUM i:D (E), of type int, evaluates to the sum of all Ei.
Formally:
Mint(SUM i : D (E),k) =
(Where Dk = ∅ means that the domain D is empty at time step k.)
-
11.
- (QuantProd) PROD i:D (E), of type int, evaluates to the product of all Ei.
Formally:
Mint(PROD i : D (E),k) =
(Where Dk = ∅ means that the domain D is empty at time step k.)
-
12.
- (QuantMin) $min i:D (E), of type int, selects the minimum of all Ei.
Formally:
Mint($min i : D (E),k) =
(Where Dk = ∅ means that the domain D is empty at time step k.)
-
13.
- (QuantMax) $max i:D (E), of type int, selects the maximum of all Ei.
Formally:
Mint($max i : D (E),k) =
(Where Dk = ∅ means that the domain D is empty at time step k.)
-
14.
- (QuantSelectDefault) The optional <rhs>, separated by a comma from the
<expr>, of a <quantif_expr> with the SELECT operator, denotes the default
value, of scalar, tuple or collection type, to select.
-
15.
- (QuantSelectType) The type Tval of the selected value of
SELECT i1 : D1, i2 : D2,…in : Dn (E [,R]) is defined as follows:
where:
The type T of the SELECT expression itself is equal to Tval if there is no default
value R. Otherwise, it is defined as the union type (see 8.4.3) of Tval and the type
of R
-
16.
- (QuantSelectDomain) The domain D of SELECT i1 : D1, i2 : D2,…in : Dn (E [,R])
is the n-fold Cartesian product D = D1 ×D2 ×…×Dn.
Note that the domain of a selection is a static subset of the type Tval defined by
(QuantSelectType) above.
-
17.
- (QuantSelectWithoutDefault) At each time step, the selection expression
SELECT i1 : D1, i2 : D2,…in : Dn (E) of type T and domain D as given
according to (QuantSelectType) and (QuantSelectDomain) respectively,
selects the unique value (if n = 1) or tuple value (if n > 1) from the
domain D for which the Boolean predicate E is true. To simplify the
formal definition below, we will extend the tuple notation to scalar
values so that V@0 will mean the same thing as V if the value V is scalar.
Formally:
MT(SELECT i1 : D1, i2 : D2,…in : Dn (E),k) =
-
18.
- (QuantSelectWithDefault) The selection expression with a default value is
similar to the selection without default (see (QuantSelectWithoutDefault)),
except in the case where no value in the domain D makes the predicate true at
time step k. In that case the default value is selected for time step k. A default
value which is a <collection> is then interpreted as a tuple value.
Formally:
MT(SELECT i1 : D1, i2 : D2,…in : Dn (E,R),k) =
(Where the cases should be considered in order from top to bottom.)
Static Flag
-
1.
- (QuantExprStaticFlag) 𝒮ℱ(<quantif_expr>) = 0.
-
2.
- (QuantVarStaticFlag) The static flag of a quantifier variable i : D (the
<id> of a <quantif_var>) is:
Restrictions
-
1.
- (QuantVarUnicity) Two quantifier variables of a quantifier expression may
not have the same name.
-
2.
- (QuantDomainFinite) Quantification is not allowed over an infinite domain.
-
3.
- (QuantDomainNotNil) Quantification is not allowed over a domain taking
the value nil in any time step (see (DomainAsRange)).
-
4.
- (QuantDomainStatic) 𝒮ℱ(D) ≥ 1 for a <quantif_var> i : D, where D is
a <domain>.
-
5.
- (ItemsOperandArrayOrFunction) The operand E of $items(E) must be
either of array type, or of function type (with a finite domain).
-
6.
- (BoolQuantOperandBool) The operand E of QTF V (E) where
QTF ∈{SOME,ALL} shall be of type bool.
-
7.
- (IntQuantOperandInt)
The operand E of QTF V (E) where QTF ∈{SUM,PROD,$min,$max} shall be
of integer type.
-
8.
- (SelectQuantOperandBool) The operand E of SELECT V1,…Vn (E [,R]) shall
be of type bool.
-
9.
- (SelectQuantDefaultCompatible) The operand
R of SELECT V1,…Vn (E [,R]) shall be of a type compatible to the type Tval
of the selected value as defined by (QuantSelectType).
-
10.
- (SelectQuantDefaultGround) The operand R of SELECT V1,…Vn (E,R) shall
not make reference to any of the quantifier variables V1 to Vn. (The following
is not allowed: SELECT i:[0,10] (false, i).)
-
11.
- (SelectQuantNoItemsDomain) A quantifier expression with operator
SELECT is not allowed in combination with a domain on the
form $items(E). In other words, the quantifier variables Vi of
SELECT V1,…Vn (E [,R]) may not be on the form i : $items(E).
11 Declarations
Declarations declare streams with a name and a type. The declared stream is visible
everywhere (except where it is hidden) in the scope where the declaration appears, regardless
of the position of the declaration within the scope. An example, where all occurrences of x
refer to the same variable:
Outputs:
x;
Definitions:
x := true;
Declarations:
bool x; // declares x of type bool in the global top-level scope
Another, more elaborate, example, which illustrates the hiding mechanism:
Outputs:
x;
Definitions:
x := true;
Declarations:
bool x;
Namespaces:
NS1 {
Outputs:
x; // Refers to the local x
Declarations:
bool x; // Hides the global x in the scope of NS1
}
NS2 {
Outputs:
x; // Refers to the global x
}
Whether the text is parsed as a <declaration> or as an <input> depends on the context, i.e. whether it
occurs in a “declarations section” (<decl_section>) or in an “inputs section” (<inputs_section>) (see
Section 16).
Syntax
(DeclarationSyntax)
<declaration> ::= [<type>] <declarator> {"," <declarator>}
<input> ::= [<type>] <input_declarator>
{"," <input_declarator>}
<input_declarator> ::= <declarator>
| "I" "(" <declarator> ")"
Semantics
-
1.
- (Declaration) A Declaration (<declaration> or <input>) declares a
stream with name and type and makes it visible everywhere in its scope (of
the namespace of streams), regardless of the position of the declaration.
-
2.
- (DeclMultInline) T D1, D2,…Dn is equivalent to the n declarations T D1,
T D2, …T Dn, regardless of whether the Di denote <declarator> or
<input_declarator>.
-
3.
- (DeclNormal) A <declaration> [T] D declares a (normal) stream
variable. The name of the variable corresponds to the first <id> of the
declarator D and the Declared Type is calculated according to procedure
calc_type in Section 7 using the base type T if given and the declarator
D. If no base type T is given, the base type used to calculate the declared
type is the type bool.
-
4.
- (DeclInput) An Input declaration (<input>) on the form [T] D (i.e. not
an initial input declaration as defined in (DeclInitialInput)) is reducible to
a normal declaration (<declaration>) [T] D. (Note the extra restrictions
(InputsFinite) and (InputsUndefined) which apply to input declarations.)
-
5.
- (DeclInitialInput) An input declaration (<input>) on the form [T] I(D)
is called an Initial input declaration and is reducible to the
normal declaration (<declaration>) [T] D. (Note the extra restriction
(DeclInitialInputDefNext) which applies to initial input declarations in
addition to those for ordinary input declarations.)
Restrictions
-
1.
- (DeclUnicity) A stream variable may not be declared more than once per
scope of the namespace of streams.
-
2.
- (InputsFinite) The resulting type (as calculated by calc_type from the
base type and the declarator) of an input declaration shall be either scalar or
composite with a finite number of components (either directly or indirectly
via other composite components).
-
3.
- (InputsUndefined) A stream declared using an input declaration
may not be defined, except for initial inputs as specified in
(DeclInitialInputDefNext).
-
4.
- (DeclInitialInputDefNext) A stream variable declared using an initial input
declaration shall be defined with, and only with, a next definition (see
Section 12).
-
5.
- (UndefinedSized) A stream declared (using a normal or an input
declaration) but not defined shall be declared using a type that is neither
int (without a size restriction), nor a composite type with a component of
type int (either directly or indirectly via other composite components).
12 Definitions
Definitions define one or several stream variables on the left hand side of the definition symbol
:= using an expression or a collection on the right hand side. If the stream variables are
undeclared they become implicitly declared by the definition, but only if the type of the right
hand side is scalar.
Multiple definitions and circular (non-causal) definitions are not allowed. For example:
Definitions:
z := x + y;
x := z - y; // Not allowed to define x or z in terms of themselves
y := 10;
y := 4; // Not allowed to define y more than once
X(w) := w; // Allowed: w keeps its value in the next cycle
If the definition is paired with a declaration, the pair must appear in the same scope. An
example:
Declarations:
bool x; // Global and undefined x
Namespaces: N {
Definitions: x := true; // Implicitly declares and defines a local x
}
Proof Obligations:
x; // The PO is falsifiable
Syntax
(DefinitionSyntax)
<definition> ::= <lhs> ":=" <rhs>
| "I" "(" <lhs> ")" ":=" <rhs>
| "X" "(" <lhs> ")" ":=" <rhs>
| <lhs> ":=" <rhs> "," <rhs>
<lhs> ::= <unfolding>
| <id> {<formal_param>}+
<rhs> ::= <expr>
| <collection>
<collection> ::= "{" <rhs> {"," <rhs>} "}"
<unfold_lhs> ::= <id> | "_"
<unfolding> ::= <unfold_lhs> {"," <unfold_lhs>}
Semantics
-
1.
- (Definition) A Definition (<definition>) defines one or several stream
variables on the Left hand side (<lhs>) using an expression or collection on
the Right hand side (<rhs>).
-
2.
- (DefUndeclared) If a stream variable on the left hand side of a
<definition> is undeclared in the scope (excluding ascendant and
descendant scopes) of the definition, then it is implicitly declared by the
definition and becomes visible everywhere in the scope (of the namespace of
streams) of the definition, regardless of the position of the definition. The
type of the variable is inferred according to (DefUndeclaredType) below.
-
3.
- (DefUndeclaredType) A stream variable V which is implicitly declared by
a definition according to (DefUndeclared) above is assigned the type T
according to the following table. TE denotes the type of the right hand side
E.
| | |
| Definition | Condition | T |
| | |
| | |
| X(V) := E | (none) | bool |
| | |
| V := E1, E2 | (none) | bool |
| | |
|
V := E | V is defined (directly or indirectly) | bool |
| | in terms of itself (recursive definition) | |
|
|
|
| | otherwise | T
E |
| | |
-
4.
- (DefAlways) V := E (always definition) where E is a stream expression
of type TE and V is a stream variable of type T, defines the value of V
in all time steps, using the expression E. Formally, for all time steps
k:
-
5.
- (DefInit) I(V) := E (initial definition) defines the value of V of type T, in the
first time step only, using the expression E of type TE. Formally:
-
6.
- (DefNext) X(V) := E (next definition) defines the value of V of type T, in the
next time step, using the expression E of type TE. Formally, for all time steps
k:
-
7.
- (DefLatch) <lhs> := E1, E2 (latch definition) is equivalent to the two
definitions I(<lhs>) := E1 and X(<lhs>) := E2.
-
8.
- (DefFunctionInit) I(V FP):= E is equivalent to the two definitions: I(V):= V′
and V′ FP:= E where V′ is a fresh variable of same type as V.
-
9.
- (DefFunctionNext) X(V FP):= E is equivalent to the two definitions:
X(V):= V′ and V′ FP:= E where V′ is a fresh variable of same type as
V.
-
10.
- (DefArrayFunction) An Array or Function definition V FP := E is equivalent to
V := lambda DS : FP := E where DS is obtained by solving the equation
TV = calc_type(TE,DS) where TV is the declared type of V and TE is the type of
E.
-
11.
- (DefCollectionRhs) A <lhs> of ordered composite type may be defined using a
collection (<collection>) on the right hand side. In such a case component
number k of <lhs> is defined by the <rhs> number k of the collection. Such
components may themselves be recursively defined by collections, if they are of
ordered composite type. Formally, a definition V := {R1,…Rn} is equivalent to
V := ((lambda[1] : [i] := V′) with [0] := {R1,…Rn})[0] where V′ is a fresh
variable with the same type as V.
The type of a <rhs> which is a <collection> is a collection type as defined in
Section 8.4.1.
-
12.
- (DefUnfolding) An Unfolding definition is a definitions where several variables
or wildcards ("_") occur comma-separatedly on the left hand side (using an
<unfolding>). If the right hand side is of composite type (including
collections) with n ordered components then such a definition with k
variables and l wildcards, with n = k + l on the left hand side is equivalent
to k ordinary definitions (i.e. with a single variable on the left hand
side) of the appropriate kind (“always”, “initial” or “next”) where the
variable at index i (with 1 ≤ i ≤ n) on the left hand side is defined
using the component (or collection element) number i on the right hand
side.
Static Flag
-
1.
- (CollectionStaticFlag) 𝒮ℱ(<collection>) = 0.
-
2.
- (DefAlwaysStaticFlag) 𝒮ℱ(V) = min(1,𝒮ℱ(E)) for V := E.
-
3.
- (DefLatchStaticFlag) 𝒮ℱ(V) = 0 for X(V) := E or V := E1, E2.
Restrictions
-
1.
- (DefCausality) A scalar stream variable or component may not have its
value in time step n be defined, directly or indirectly, in terms of its own
value in any time step k ≥ n.
The cyclicity criterion, i.e. the precise criterion for when such a variable or
component is considered defined in terms of its own value will depend on
the reasoning power of tools implementing HLL – especially when it comes
to recursive array and function definitions – and is thus outside the scope
of this document.
-
2.
- (DefUnicity) A stream variable may not have its value in time step n be
defined more than once.
-
3.
- (DefCompleteness) A stream variable with an initial definition shall also
have a next definition. (The converse is not required however, i.e. the initial
value may be left undefined/free.)
-
4.
- (DefUndeclaredLhsScalarRhs) If the variable on the <lhs> is undeclared,
then there shall be no <formal_param> and the type of the <rhs> shall be
scalar.
-
5.
- (DefRhsTypeAssignableToLhsType) The type of the <rhs> shall be
assignable to the type of the <lhs>. For this purpose, the type of an <lhs>
on the form V FP (where FP corresponds to the {<formal_param>}+) is
derived in the same way as for the corresponding projection expression (see
Section 10.6).
-
6.
- (LatchesSized) A stream defined with a latch or next definition shall not
be declared with a type that is either int (without a size restriction), or a
composite type with a component of type int (either directly or indirectly
via other composite components).
-
7.
- (DefUnfoldingCompatibleRhs) When the left hand side (<lhs>) of a
definition is on the form of an <unfolding>, then the right hand
side (<rhs>) shall be of ordered composite type, but shall not be of
multidimensional array type nor of multivariate function type, and the
number of variables plus the number of wildcards on the left hand side shall
equal the number of components of the type of the right hand side.
13 Constants
Syntax
(ConstantSyntax)
<constant> ::= "bool" <id> ":=" <expr>
| "int" <id> ":=" <expr>
Semantics
-
1.
- (ConstantDef) A Constant definition (<constant>) declares and defines a
named constant stream.
-
2.
- (ConstantDefIsaDeclDef) Semantically, T C := E is equivalent to:
Declarations:
T C;
Definitions:
C := E;
Furthermore, all restrictions that apply to the latter language construct also
apply to the former (as according to (ConstantDefInheritedRestrictions)).
However, there are two minor differences between the language constructs:
-
(a)
- The static flag of C as defined by the former construct is 2 (as according
to (ConstantStaticFlag)), whereas it is at most 1 for the C defined
by the latter construct (as according to (DefAlwaysStaticFlag) of
Section 12).
-
(b)
- The additional restriction (ConstantDefRhsConstant) applies only to
the former construct.
Static Flag
-
1.
- (ConstantStaticFlag) 𝒮ℱ(C) = 2 for a <constant> T C := E.
Restrictions
-
1.
- (ConstantDefRhsConstant) 𝒮ℱ(E) = 2 for a <constant> T C := E.
-
2.
- (ConstantDefInheritedRestrictions) All restrictions that apply to the language
construct:
Declarations:
T C;
Definitions:
C := E;
also apply to a <constant> T C := E.
14 Constraints
Syntax
(ConstraintSyntax)
<constraint> ::= <expr>
| "I" "(" <expr> ")"
Semantics
-
1.
- (ConstraintAlways) An Always constraint E (an <expr>) corresponds to
the proposition □E.
-
2.
- (ConstraintInitial) An Initial constraint I(E) corresponds to the
proposition 𝕀 E.
Restrictions
-
1.
- (ConstraintBool) Constraints shall be expressions of type bool.
15 Proof Obligations
Syntax
(PoSyntax)
<po> ::= <expr>
Semantics
-
1.
- (PoBool) A Proof obligation (PO) E (an <expr>) of type bool corresponds
to the proposition □E.
-
2.
- (PoComposite) A proof obligation E of type T, which is an array or
function type with bool as component type, corresponds to the proposition
□( ALL e : $items(E) (e) ).
-
3.
- (PoValid) A proof obligation is Valid iff it is a consequence of all the
constraints within the same (global) HLL text (regardless of whether the
constraints appear in the same user namespace or not). Note that if there
is no model M which does not falsify the constraints (for example if the
constraints are contradictory), then any proof obligation is trivially valid.
-
4.
- (PoFalsifiable) A proof obligation which is not valid takes the value nil or
the value false at some time step k in some model M which does not
falsify the constraints. If the proof obligation takes the value nil we say
that the proof obligation is not well-defined. Otherwise, if it takes the value
false, we say that the proof obligation is Falsifiable.
Restrictions
-
1.
- (PoType) Proof obligations shall be expressions of type bool, or of array
or function type with bool as component type. (This means that the types
bool^(N) or bool^(N, M) are accepted but not the type bool^(N)^(M).)
16 Sections
Syntax
(SectionSyntax)
<HLL> ::= {<section>}
<section> ::= <constants_section>
| <types_section>
| <inputs_section>
| <decl_section>
| <def_section>
| <outputs_section>
| <constr_section>
| <po_section>
| <namespaces_section>
<constants_section> ::= <constants> ":" {<constant> ";"}
<types_section> ::= <types> ":" {<type_def> ";"}
<inputs_section> ::= <inputs> ":" {<input> ";"}
<decl_section> ::= <declarations> ":" {<declaration> ";"}
<def_section> ::= <definitions> ":" {<definition> ";"}
<outputs_section> ::= <outputs> ":" {<expr> ";"}
<constr_section> ::= <constraints> ":" {<constraint> ";"}
<po_section> ::= <proof> <obligations> ":" {<po> ";"}
<namespaces_section> ::= <namespaces> ":" {<namespace>}
<constants> ::= "Constants" | "constants"
<types> ::= "Types" | "types"
<inputs> ::= "Inputs" | "inputs"
<declarations> ::= "Declarations" | "declarations"
<definitions> ::= "Definitions" | "definitions"
<constraints> ::= "Constraints" | "constraints"
<proof> ::= "Proof" | "proof"
<obligations> ::= "Obligations" | "obligations"
<outputs> ::= "Outputs" | "outputs"
<namespaces> ::= "Namespaces" | "namespaces"
Semantics
-
1.
- (HLLText) An HLL text (<HLL>) is a (possibly empty) list of sections.
-
2.
- (GlobalTopLevelScopes) The Global top-level scopes of an HLL text <HLL>
that is not nested within a <namespace> encompass the entire text.
-
3.
- (SectionOrderIrrelevant) The order of the sections of an HLL text and the
order of items within the sections have no impact on the semantics of the
text.
-
4.
- (SectionsReopen) Sections may be opened any number of times.
Restrictions
-
1.
- (OutputsFinite) The <expr> in an <outputs> section shall be either of
scalar type or of a composite type with a finite number of scalar components
(either directly or indirectly via other composite components).
A Syntax Overview
______________________________________________________
<HLL> ::= {<section>}
<section> ::= <constants_section>
| <types_section>
| <inputs_section>
| <decl_section>
| <def_section>
| <outputs_section>
| <constr_section>
| <po_section>
| <namespaces_section>
<constants_section> ::= <constants> ":" {<constant> ";"}
<types_section> ::= <types> ":" {<type_def> ";"}
<inputs_section> ::= <inputs> ":" {<input> ";"}
<decl_section> ::= <declarations> ":" {<declaration> ";"}
<def_section> ::= <definitions> ":" {<definition> ";"}
<outputs_section> ::= <outputs> ":" {<expr> ";"}
<constr_section> ::= <constraints> ":" {<constraint> ";"}
<po_section> ::= <proof> <obligations> ":" {<po> ";"}
<namespaces_section> ::= <namespaces> ":" {<namespace>}
<constants> ::= "Constants" | "constants"
<types> ::= "Types" | "types"
<inputs> ::= "Inputs" | "inputs"
<declarations> ::= "Declarations" | "declarations"
<definitions> ::= "Definitions" | "definitions"
<constraints> ::= "Constraints" | "constraints"
<proof> ::= "Proof" | "proof"
<obligations> ::= "Obligations" | "obligations"
<outputs> ::= "Outputs" | "outputs"
<namespaces> ::= "Namespaces" | "namespaces"
<namespace> ::= <id> "{" <HLL> "}"
<constant> ::= "bool" <id> ":=" <expr>
| "int" <id> ":=" <expr>
<type_def> ::= <type> <declarator> {"," <declarator>}
| <enum_def>
| <sort_def>
<declarator> ::= <id> {<declarator_suffix>}
<declarator_suffix> ::= "[" <expr_list> "]"
| "(" <type_list> ")"
<type> ::= "bool"
| <integer>
| <tuple>
| <structure>
| <array>
| <function>
| <named_type>
<integer> ::= "int"
| "int" <sign>
| "int" <range>
<sign> ::= "signed" <id_or_int>
| "unsigned" <id_or_int>
<id_or_int> ::= <id>
| <int_literal>
<range> ::= "[" <expr> "," <expr> "]"
<enum_def> ::= <enumerated> <id>
<enumerated> ::= "enum" "{" <id_list> "}"
<tuple> ::= "tuple" "{" <type_list> "}"
<structure> ::= "struct" "{" <member_list> "}"
<sort_def> ::= "sort" [ <sort_contrib> "<" ] <id>
<sort_contrib> ::= <path_id_list>
| "{" <id_list> "}"
<array> ::= <type> "^" "(" <expr_list> ")"
<function> ::= "(" <type> {"*" <type>} "->" <type> ")"
<named_type> ::= <path_id>
<type_list> ::= <type> {"," <type>}
<member_list> ::= <id> ":" <type> {"," <id> ":" <type>}
<input> ::= [<type>] <input_declarator>
{"," <input_declarator>}
<input_declarator> ::= <declarator>
| "I" "(" <declarator> ")"
<declaration> ::= [<type>] <declarator> {"," <declarator>}
<po> ::= <expr>
<constraint> ::= <expr>
| "I" "(" <expr> ")"
<definition> ::= <lhs> ":=" <rhs>
| "I" "(" <lhs> ")" ":=" <rhs>
| "X" "(" <lhs> ")" ":=" <rhs>
| <lhs> ":=" <rhs> "," <rhs>
<lhs> ::= <unfolding>
| <id> {<formal_param>}+
<rhs> ::= <expr>
| <collection>
<collection> ::= "{" <rhs> {"," <rhs>} "}"
<unfold_lhs> ::= <id> | "_"
<unfolding> ::= <unfold_lhs> {"," <unfold_lhs>}
<formal_param> ::= "[" <id_list> "]"
| "(" <id_list> ")"
<accessor> ::= "." <id>
| "." <int_literal>
| "[" <expr_list> "]"
| "(" <expr_list> ")"
<expr> ::= <ite_expr>
| <lambda_expr>
| <binop_expr>
| <membership_expr>
| <unop_expr>
| <proj_expr>
<ite_expr> ::= "if" <expr> "then" <expr>
{"elif" <expr> "then" <expr>}
"else" <expr>
<lambda_expr> ::= "lambda" {<declarator_suffix>}+ ":"
{<formal_param>}+ ":=" <expr>
<binop_expr> ::= <expr> <binop> <expr>
<membership_expr> ::= <expr> ":" <domain>
<domain> ::= <range>
| <type_domain>
<type_domain> ::= <named_type>
| "bool"
| "int"
<unop_expr> ::= <unop> <expr>
<proj_expr> ::= <closed_expr> { <accessor> }
<closed_expr> ::= <bool_literal>
| <int_literal>
| <named_expr>
| <next_expr>
| <pre_expr>
| <fun_expr>
| <cast_expr>
| <with_expr>
| <case_expr>
| <quantif_expr>
| "(" <expr> ")"
<bool_literal> ::= <true>
| <false>
<dec_literal> ::= [0-9](_?[0-9])*
<bin_literal> ::= 0[Bb][0-1][_?[0-1])*
<hex_literal> ::= 0[Xx][0-9A-Fa-f](_?[0-9A-Fa-f])*
<int_literal> ::= <dec_literal>
| <hex_literal>
| <bin_literal>
<named_expr> ::= <path_id>
<next_expr> ::= "X" "(" <expr> ")"
<pre_expr> ::= ("pre" | "PRE") ["<" <type> ">"]
"(" <expr> ["," <expr>] ")"
<fun_expr> ::= <fop> "(" <expr_list> ")"
<cast_expr> ::= "cast" "<" <type> ">" "(" <expr> ")"
<with_expr> ::= "(" <expr> "with" {<accessor>}+ ":=" <rhs> ")"
<case_expr> ::= "(" <expr_list> {<case_item>}+ ")"
<case_item> ::= "|" <pattern_list> "=>" <expr>
<pattern> ::= <expr>
| <named_type> ( <id> | "_" )
| "_"
<pattern_list> ::= <pattern> { "," <pattern> }
<quantif_expr> ::= <quantifier> <quantif_vars>
( "(" <expr> ")" | <quantif_expr> )
| "SELECT" <quantif_vars>
( "(" <expr> ["," <rhs>] ")" |
<quantif_expr> )
<quantif_vars> ::= <quantif_var> {"," <quantif_var>}
<quantif_var> ::= <id> ":" <quantif_domain>
<quantif_domain> ::= <domain>
| "$items" "(" <expr> ")"
<binop> ::= "#" | "&" | "#!" | "->" | "<->"
| ">" | ">=" | "<" | "<="
| "=" | "==" | "!=" | "<>"
| "+" | "-" | "*" | "%" | "^" | "<<" | ">>"
| "/" | "/>" | "/<"
<unop> ::= "~" | "-"
<fop> ::= "$min"
| "$max"
| "$abs"
| "$or"
| "$and"
| "$xor"
| "$not"
| "bin2u"
| "u2bin"
| "bin2s"
| "s2bin"
| "population_count_eq"
| "population_count_lt"
| "population_count_gt"
<expr_list> ::= <expr> {"," <expr>}
<id_list> ::= <id> {"," <id>}
<path_id_list> ::= <path_id> {"," <path_id>}
<path_id> ::= <relative_path> <id>
| <absolute_path> <id>
<relative_path> ::= { <id> "::" }
<absolute_path> ::= "::" { <id> "::" }
<id> ::= regexp: [a-zA-Z_][a-zA-Z0-9_]*
| regexp: ’[^\n’]+’
| regexp: "[^\n"]+"
<true> ::= "true" | "TRUE" | "True"
<false> ::= "false" | "FALSE" | "False"
<quantifier> ::= "SOME" | "ALL" | "SUM" | "PROD"
| "CONJ" | "DISJ" | "$min" | "$max"
A.1 Operator Precedence and Associativity
The precedence of expressions is given below in order from lowest to highest (same line means
same precedence). The information below is a copy of (ExprPrecedence).
-
1.
- <ite_expr>, <lambda_expr>
-
2.
- <binop_expr>, <membership_expr>
-
3.
- <unop_expr>
-
4.
- <proj_expr>
The precedence of the binary operators is given below in order from lowest to highest,
together with their associativity. Same line means same precedence. The information below is
a copy of (BinopGrouping).
| | Precedence | Associativity |
| | <-> #! | left |
| | -> | right |
| | # | left |
| | & | left |
| | > >= < <= = == != <> | left |
| | << >> | left |
| | + - | left |
| | * / /< /> % | left |
| | ^ | right |
| | |
B Reserved Words
_______________________________________________________
ALL
assumptions
Assumptions
bin2s
bin2u
block
blocks
Blocks
bool
cast
CONJ
constants
Constants
constraints
Constraints
declarations
Declarations
definitions
Definitions
DISJ
elif
else
enum
false
False
FALSE
guarantees
Guarantees
I
if
inputs
Inputs
int
lambda
namespaces
Namespaces
new
obligations
Obligations
outputs
Outputs
population_count_eq
population_count_gt
population_count_lt
pre
PRE
PROD
proof
Proof
s2bin
SELECT
signed
SOME
sort
struct
SUM
then
true
True
TRUE
tuple
types
Types
u2bin
unsigned
with
X
C Restrictions Overview
Below are listed the direct and indirect restrictions which apply to each language construct of
HLL. The indirect restrictions, as explained in Section 2.4.2, are due to language constructs
being defined by translation or reduction to other language constructs which in turn
have restrictions on them. These restrictions also apply, indirectly, to the language
constructs defined by the translation or reduction, and are thus listed in the table
below.
On the other hand, some language constructs contain sub-constructs which have specific
restrictions applied to them. The restrictions which apply to sub-constructs are not listed as
applicable to the parent construct (to avoid duplication). An example is projections,
<proj_expr>, which are defined using the sub-construct <accessor> where specific
restrictions apply.
When a restriction applies only to a certain part of a language construct, we will occasionally,
for the benefit of the reader and especially if the restriction is indirect, prefix the restriction
with the part of the language construct to which it applies.
| Language Construct | Parent Construct | Applicable Restrictions |
|
|
| s2bin(E1, E2) | <fun_expr> | (FunopBinaryCard) |
| | | E1: (ProjAccCompatible) |
| | | E1: (IntCoreBinopOperandsInt) |
| | | E2: (DeclArrayDimInteger) |
| | | E2: (DeclArrayDimConstant) |
| population_count_lt(E1,…En,K) | <fun_expr> | (PopCountNumberStatic) |
| | | Ei: (IteCondBool) |
| | | K: (IntCoreBinopOperandsInt) |
| population_count_gt(E1,…En,K) | <fun_expr> | (PopCountNumberStatic) |
| | | Ei: (IteCondBool) |
| | | K: (IntCoreBinopOperandsInt) |
| population_count_eq(E1,…En,K) | <fun_expr> | (PopCountNumberStatic) |
| | | Ei: (IteCondBool) |
| | | K: (IntCoreBinopOperandsInt) |
| <cast_expr> | | (CastTargetIntImpl) |
| | | (ProjAccCompatible) |
| | | (IntCoreBinopOperandsInt) |
| <with_expr> | | (WithAccCompatible) |
| | | (WithRhsAssignable) |
| <case_expr> | | (CaseSwitchesScalar) |
| | | (CasePatternsCompatible) |
| | | (CaseBranchesCompatible) |
| | | (CasePatternExprConstant) |
| | | (CasePatternTypeSort) |
| | | (CaseCapturingVarUnicity) |
| SOME i1 : D1,…in : Dn (E) | <quantif_expr> | (QuantVarUnicity) |
| | | (QuantDomainFinite) |
| | | (QuantDomainNotNil) |
| | | (QuantDomainStatic) |
| | | (BoolQuantOperandBool) |
| ALL i1 : D1,…in : Dn (E) | <quantif_expr> | (QuantVarUnicity) |
| | | (QuantDomainFinite) |
| | | (QuantDomainNotNil) |
| | | (QuantDomainStatic) |
| | | (BoolQuantOperandBool) |
| DISJ i1 : D1,…in : Dn (E) | <quantif_expr> | (QuantVarUnicity) |
| | | (QuantDomainFinite) |
| | | (QuantDomainNotNil) |
| | | (QuantDomainStatic) |
| | | (BoolQuantOperandBool) |
| | |
D Glossary
For the purposes of this document, the following terms and abbreviations are used.
-
1.
- ascendant scope
an enclosing scope, i.e. one higher up in the scope stack; see Section 2.3
-
2.
- ASCII
American Standard Code for Information Interchange, a character encoding
standard
-
3.
- assignable / assignability
refers to the assignability relation between types, see Section 8; a stream
expression E1 is assignable to a stream expression E2 iff the type of E1 is
assignable to the type of E2
-
4.
- combinatorial function
a mapping from values to values (usually a mapping from one or several
values to a single value)
-
5.
- combinatorial operator
see combinatorial function
-
6.
- compatible / compatibility
(sometimes preceded by type) refers to the compatibility relation between
types, see Section 8; a stream expression E1 is compatible with a stream
expression E2 iff the type of E1 is compatible with the type of E2
-
7.
- component
either a component (type) of a composite type, or a component (stream) of a
stream of composite type; similar terms used elsewhere would be e.g. struct
field, array element, function output – all those entities are collectively
called components in this document
-
8.
- composite
equivalent to non-scalar;
(noun) a stream of composite type
(adj.) applied to a stream it means a composite stream; applied to a type it
means a composite type; applied to a value it means a value of a composite
type
-
9.
- composite type
equivalent to non-scalar type; any type defined in Section 8.2
-
10.
- consequence
see Section 2.1.4
-
11.
- constant
refers either to a stream defined using the nonterminal <constant> of
Section 13, or to any stream with a static flag of 2.
-
12.
- declared type
see Section 11
-
13.
- defined variable
a variable with a definition, i.e. that occurs on the left hand side of a
definition; see Section 12
-
14.
- descendant scope
an enclosed scope, i.e. one further down in the scope stack; see Section 2.3
-
15.
- directly defined
(adj.) refers to an entity E1 which is defined in terms of another entity E2
without there being any intermediate entity E3 in between E1 and E2; see
also indirectly defined
-
16.
- domain
depending on the context, refers to one of:
-
(a)
- the nonterminal <domain>, defined in Section 10.4,
-
(b)
- the nonterminal <quantif_domain>, defined in Section 10.7.10,
-
(c)
- the parameter types of a function type, see Section 8.2.3,
-
(d)
- the domain of an array type, which amounts to the parameter types
of the equivalent function type, see Section 8.2.4, or
-
(e)
- the domain of the SELECT operator, which is defined by
(QuantSelectDomain).
-
17.
- EBNF
Extended Backus-Naur Form, see also Section 2.4.1
-
18.
- equivalent to
see Section 2.4.2
-
19.
- explicit grouping
the process of adding parentheses around all subexpressions (or groups) in a
text; for example, expressions such as “a & b & c” and “a + b * c” are
explictly grouped into respectively “((a & b) & c)” and “(a + (b * c))”
-
20.
- free
(adj.) applied to a variable it means a variable that is free to take any value of
its type in each time step; input variables are free; quantifier variables or defined
variables are not free
-
21.
- fresh
(adj). applied to the identifier of an entity it means that another entity with the
same identifier is not visible within the same namespace; (an entity with a fresh
name does not hide another entity)
-
22.
- function accessor
see (AccFunction) of Section 9
-
23.
- function value
see combinatorial function
-
24.
- group / grouping
see implicit grouping or explicit grouping
-
25.
- hide / hiding
refers to variable hiding see Section 2.3
-
26.
- HLL
High Level Language
-
27.
- HLL function
a stream of combinatorial functions (function values) which, together with a
function accessor, maps streams to streams by point-wise application of the
combinatorial function in each time step on the values of the stream operands in
the same time step; HLL functions are distinct from temporal functions which
are general mappings of streams to streams
-
28.
- iff
if and only if
-
29.
- implicit grouping
the process by which a parser uses syntax, precedence and associativity rules to
map a text into an abstract syntax tree (AST) where each group (or
subexpression) is represented by its own vertex
-
30.
- implicit input
(sometimes followed by variable) a free variable that is not an (explicit)
input
-
31.
- indirectly defined
(adj.) refers to an entity E1 which is defined in terms of another entity E2 via an
intermediate entity E3; e.g. E1 := E3; E3 := E2;
-
32.
- initial input
(sometimes followed by variable) a memory variable which is undefined in the
first time step (i.e. it has only a next definition, see Section 12)
-
33.
- input
(sometimed preceded by explicit; sometimes followed by variable) refers to
variables declared using the nonterminal <input>, see Section 11
-
34.
- integer implementation type
see Related Notation 1 of Section 8.1.2
-
35.
- integer range type
see Related Notation 2 of Section 8.1.2
-
36.
- integer type
any type defined in Section 8.1.2
-
37.
- latch
(sometimes followed by variable) a variable defined using a latch or a next
definition, see Section 12
-
38.
- literal
(sometimes followed by value) refers to an immediate value such as the integer
literal 1234 or the Boolean literal true.
-
39.
- memory
either a pre expression or a latch; if followed by variable it means a
latch.
-
40.
- model
(sometimes preceded by stream) see Section 2.1.1.
-
41.
- multidimensional
(adj). applied to an array type it means that the type has more than one
dimension, see Section 8.2.4
-
42.
- multivariate
(adj). applied to a function type it means that the type has more than one
parameter type, see Section 8.2.3
-
43.
- namespace
see Section 2.3; not to be confused with user namespace
-
44.
- nil
see Section 2.1.2
-
45.
- parameter
refers to the nonterminal <formal_param> defined in Section 10.2
-
46.
- proposition
see Section 2.1.3
-
47.
- qualified
(adj). applied to a path identifier (<path_id>) it means a path identifier with at
least one occurrence of "::". See Section 5.1
-
48.
- reducible to
see Section 2.4.2
-
49.
- scalar
(noun) a stream of scalar type
(adj.) applied to a stream it means a scalar stream; applied to a type it
means a scalar type; applied to a value it means a value of a scalar
type
-
50.
- scalar type
any type defined in Section 8.1
-
51.
- scope
see Section 2.3
-
52.
- significant bit
a significant bit of an integer encoded in two’s complement is a bit which cannot
be removed from the encoding without changing the encoded value; leading 0s
and 1s are not significant, meaning that the numbers 000 and 0 both
encode 0, 001 and 01 both encode +1, and 111 and 1 both encode
−1
-
53.
- static flag
see Section 2.1.5
-
54.
- stream
a stream of values of a certain type, see Section 10
-
55.
- temporal function
a mapping from streams to streams
-
56.
- temporal operator
see temporal function
-
57.
- type
a tool for the classification of streams which can be understood simply as a set of
values, see Section 8
-
58.
- undefined variable
see free variable
-
59.
- unsized copy
see Section 8.4.2
-
60.
- user namespace
see Section 5; not to be confused with namespace
-
61.
- value
a mathematical object that is the element or member of a type, for example the
Boolean value “true”, the integer value “1234”, or the enum value “blue”;
composite values (i.e. values of composite types) can be represented by n-tuples
where n corresponds to the number of components of the composite type, for
example “(true,1234)”; if a value V is used in a context where a stream is
expected, it is interpreted as a constant stream that takes the value V in each
time step
-
62.
- variable
(often preceded by stream) a stream variable, i.e. a named stream (that can be
referenced if it is visible)
-
63.
- visible / visibility
refers to variable visibility, see Section 2.3
Label Index
AccArray, 53
AccFunction, 53
AccStruct, 53
AccTuple, 53
AccessorSyntax, 53
ArrayAssignability, 47
ArrayCompatibility, 47
ArrayDimConstant, 47
ArrayDimNotNil, 47
ArrayIndexInteger, 53
ArraySyntax, 47
ArrayType, 47
ArrayValues, 47
BinopGrouping, 60
BinopStaticFlag, 60
BinopSyntax, 60
BoolAnd, 60
BoolAssignability, 35
BoolCompatibility, 35
BoolEquiv, 60
BoolImpl, 60
BoolLitFalse, 67
BoolLitStaticFlag, 67
BoolLitSyntax, 67
BoolLitTrue, 67
BoolNeg, 63
BoolNegOperandBool, 63
BoolOr, 60
BoolOrEquivOperandsBool, 60
BoolQuantOperandBool, 82
BoolSyntax, 35
BoolValueOrder, 35
BoolValues, 35
BoolXor, 60
CaseBranchesCompatible, 79
CaseCapturingVarStaticFlag, 79
CaseCapturingVarUnicity, 79
CaseCapturingVariable, 79
CaseExpr, 79
CaseExprNil, 79
CaseExprStaticFlag, 79
CaseExprSyntax, 79
CasePatternExpr, 79
CasePatternExprConstant, 79
CasePatternType, 79
CasePatternTypeSort, 79
CasePatternWildcard, 79
CasePatternsCompatible, 79
CaseSwitchesScalar, 79
CastExpr, 74
CastExprSyntax, 74
CastNamedType, 74
CastSigned, 74
CastStaticFlag, 74
CastTargetIntImpl, 74
CastUnsigned, 74
ClosedExprSyntax, 66
CollArrayAssignability, 50
CollFuncAssignability, 50
CollMultiDimArrayAssignability, 50
CollMultiVarFuncAssignability, 50
CollTupleCompatibility, 50
CollTupleStructAssignability, 50
CollectionReason, 50
CollectionStaticFlag, 88
CollectionType, 50
CommentDoubleSlash, 23
CommentSlashStar, 23
ConstantDef, 89
ConstantDefInheritedRestrictions, 89
ConstantDefIsaDeclDef, 89
ConstantDefRhsConstant, 89
ConstantStaticFlag, 89
ConstantSyntax, 89
ConstraintAlways, 90
ConstraintBool, 90
ConstraintInitial, 90
ConstraintSyntax, 90
DeclArrayDimConstant, 32
DeclArrayDimInteger, 32
DeclFunctionParamScalar, 32
DeclInitialInput, 85
DeclInitialInputDefNext, 85
DeclInput, 85
DeclMultInline, 85
DeclNormal, 85
DeclUnicity, 85
Declaration, 85
DeclarationSyntax, 85
Declarator, 32
DeclaratorSyntax, 32
DeclaratorTypeCalc, 32
DefAlways, 88
DefAlwaysStaticFlag, 88
DefArrayFunction, 88
DefCausality, 88
DefCollectionRhs, 88
DefCompleteness, 88
DefFunctionInit, 88
DefFunctionNext, 88
DefInit, 88
DefLatch, 88
DefLatchStaticFlag, 88
DefNext, 88
DefRhsTypeAssignableToLhsType, 88
DefUndeclared, 88
DefUndeclaredLhsScalarRhs, 88
DefUndeclaredType, 88
DefUnfolding, 88
DefUnfoldingCompatibleRhs, 88
DefUnicity, 88
Definition, 88
DefinitionSyntax, 88
Domain, 62
DomainAsRange, 62
DomainAsType, 62
DomainScalar, 62
Elif, 55
EmptyScalarTypeNil, 54
EnumAssignability, 38
EnumCompatibility, 38
EnumDef, 38
EnumSyntax, 38
EnumValueDef, 38
EnumValueOrder, 38
EnumValueSpace, 38
EnumValueStaticFlag, 38
EnumValueUnicity, 38
EqOperandsFiniteCompatible, 60
Expr, 54
ExprPrecedence, 54
ExprSyntax, 54
FormalParamStaticFlag, 58
FunctionAssignability, 46
FunctionCompOrder, 46
FunctionCompatibility, 46
FunctionDomainEquality, 46
FunctionDomainScalar, 46
FunctionInputScalar, 53
FunctionSyntax, 46
FunctionType, 46
FunctionValues, 46
FunopBinaryCard, 73
FunopBinaryStaticFlag, 73
FunopNaryStaticFlag, 73
FunopSyntax, 73
FunopUnaryCard, 73
FunopUnaryStaticFlag, 73
GlobalTopLevelScopes, 93
GroupedExpr, 66
GroupedExprStaticFlag, 66
HLLText, 93
Id, 25
IdOrInt, 37
IdSignificantChars, 25
IdSyntax, 25
IfThenElse, 55
InlineMultTypeDef, 34
InputsFinite, 85
InputsUndefined, 85
IntAbs, 73
IntAdd, 60
IntAssignability, 37
IntCeilDiv, 60
IntCompatibility, 37
IntCoreBinopOperandsInt, 60
IntDiv, 60
IntExp, 60
IntFloorDiv, 60
IntGt, 60
IntGte, 60
IntLeftShift, 60
IntLitBinary, 68
IntLitDecimal, 68
IntLitHexadecimal, 68
IntLitStaticFlag, 68
IntLitSyntax, 68
IntLitUnderscores, 68
IntLiteral, 68
IntLt, 60
IntLte, 60
IntMax, 73
IntMin, 73
IntMul, 60
IntNeg, 63
IntNegOperandInt, 63
IntQuantOperandInt, 82
IntRangeValues, 37
IntRem, 60
IntRightShift, 60
IntSignedValues, 37
IntSizeConstant, 37
IntSizeInteger, 37
IntSizeNotNil, 37
IntSub, 60
IntSyntax, 37
IntUnsignedValues, 37
IntValueOrder, 37
IntValues, 37
IteBranchesCompatible, 55
IteCondBool, 55
IteExprStaticFlag, 55
IteExprSyntax, 55
ItemsOperandArrayOrFunction, 82
LambdaArray, 58
LambdaDeclSuffixOverhang, 58
LambdaExprSyntax, 58
LambdaFunction, 58
LambdaMultFormalParam, 58
LambdaParamUnicity, 58
LambdaParamsBound, 58
LambdaParamsMatch, 58
LambdaScope, 58
LambdaStaticFlag, 58
LambdaType, 58
LambdaTypeCheck, 58
LatchesSized, 88
Membership, 62
MembershipDomainCompatible, 62
MembershipPrecedence, 62
MembershipStaticFlag, 62
MembershipSyntax, 62
NamedExpr, 69
NamedExprImplicitDecl, 69
NamedExprStaticFlag, 69
NamedExprSyntax, 69
NamedExprUndefinedStaticFlag, 69
NamedType, 48
NamedTypeAssignability, 48
NamedTypeCompatibility, 48
NamedTypeRef, 48
NamedTypeSyntax, 48
NamespaceSyntax, 26
NextExpr, 70
NextExprStaticFlag, 70
NextExprSyntax, 70
OpBin2s, 73
OpBin2u, 73
OpBitwiseAnd, 73
OpBitwiseNot, 73
OpBitwiseOr, 73
OpBitwiseXor, 73
OpEqCompositeMultiDim, 60
OpEqCompositeUniDim, 60
OpEqEq, 60
OpEqScalar, 60
OpNeq, 60
OpPopCountEq, 73
OpPopCountGt, 73
OpPopCountLt, 73
OpS2bin, 73
OpU2bin, 73
OutputsFinite, 93
PathAbsolute, 28
PathId, 28
PathIdLookup, 28
PathIdNoImplicitDecl, 28
PathIdSyntax, 28
PathRelative, 28
PoBool, 91
PoComposite, 91
PoFalsifiable, 91
PoSyntax, 91
PoType, 91
PoValid, 91
PopCountNumberStatic, 73
Pragma, 24
PreExprStaticFlag, 71
PreExprSyntax, 71
PreOperandsAssignable, 71
PreTyped, 71
PreTypedWithInit, 71
PreUntyped, 71
PreUntypedWithInit, 71
PreUppercase, 71
ProjAccCompatible, 65
ProjArrayFunc, 65
ProjExprNil, 65
ProjExprStaticFlag, 65
ProjExprSyntax, 65
ProjMultipleAcc, 65
Projection, 65
QuantAll, 82
QuantConj, 82
QuantDisj, 82
QuantDomainDomain, 82
QuantDomainFinite, 82
QuantDomainItems, 82
QuantDomainNotNil, 82
QuantDomainStatic, 82
QuantExprStaticFlag, 82
QuantExprSyntax, 82
QuantMax, 82
QuantMin, 82
QuantMultVar, 82
QuantProd, 82
QuantScope, 82
QuantSelectDefault, 82
QuantSelectDomain, 82
QuantSelectType, 82
QuantSelectWithDefault, 82
QuantSelectWithoutDefault, 82
QuantSome, 82
QuantSum, 82
QuantVarStaticFlag, 82
QuantVarType, 82
QuantVarUnicity, 82
RangeDomainStaticFlag, 62
ReservedWords, 25
SecondShiftOperandNonNegative, 60
SecondShiftOperandStatic, 60
SectionOrderIrrelevant, 93
SectionSyntax, 93
SectionsReopen, 93
SelectQuantDefaultCompatible, 82
SelectQuantDefaultGround, 82
SelectQuantNoItemsDomain, 82
SelectQuantOperandBool, 82
SignedBitsPositive, 37
SortAssignability, 40
SortCompatibility, 40
SortContrib, 40
SortContribScope, 40
SortDef, 40
SortSubTypeContrib, 40
SortSubTypes, 40
SortSyntax, 40
SortUnionAssignability, 52
SortUnionCompatibility, 52
SortValueContrib, 40
SortValueOrder, 40
SortValueSpace, 40
SortValueStaticFlag, 40
SortValueUnicity, 40
StructAssignability, 43
StructCompIdSpace, 43
StructCompUnicity, 43
StructCompatibility, 43
StructSyntax, 43
StructType, 43
StructValues, 43
TupleAssignability, 42
TupleCompatibility, 42
TupleSyntax, 42
TupleType, 42
TupleValues, 42
Type, 34
TypeAssignability, 34
TypeCalc, 34
TypeCompatibility, 34
TypeDef, 34
TypeDefCausality, 34
TypeDefUnicity, 34
TypeDomainStaticFlag, 62
TypeIdSpace, 34
TypeSyntax, 34
UndefinedSized, 85
UnionComposite, 52
UnionScalar, 52
UnionSort, 52
UnionTupleCollection, 52
UnopStaticFlag, 63
UnopSyntax, 63
UnsignedBitsNonNegative, 37
UnsizedComposite, 51
UnsizedInteger, 51
UnsizedScalar, 51
UserNamespace, 26
UserNamespaceName, 26
UserNamespaceScattering, 26
WithAccCompatible, 77
WithArrayAcc, 77
WithCollectionRhsMultiDim, 77
WithCollectionRhsUniDim, 77
WithExprStaticFlag, 77
WithExprSyntax, 77
WithFunctionAcc, 77
WithMultipleAcc, 77
WithRhsAssignable, 77
WithTupleStructAcc, 77
E How to Contact Prover Technology
If you have questions or comments concerning this document, or want to report an error or
omission, you are welcome to contact our support staff at:
hll-support@prover.com
For other inquiries please refer to the contact details on our Web page:
https://www.prover.com/about-us/contact-us/
We welcome your comments on our products, so please do not hesitate to contact
us.
References

 D is a semantic relation between models and propositions defined as:
D is a semantic relation between models and propositions defined as:
 D𝕀 s iff Mbool(s,0) ∈ D for Mbool ∈ M.
D𝕀 s iff Mbool(s,0) ∈ D for Mbool ∈ M.
 D□s iff Mbool(s,n) ∈ D for Mbool ∈ M and for all n.
D□s iff Mbool(s,n) ∈ D for Mbool ∈ M and for all n. D, written
D, written  w, uses the definition above with D = {true,nil}, and the
strong variant, written
w, uses the definition above with D = {true,nil}, and the
strong variant, written  s, uses the definition above with D = {true}. We note
that if the streams underlying the propositions in P ∪{q} are all well-defined in all
time steps of all models, then this distinction in a weak and a strong case becomes
unnecessary.
s, uses the definition above with D = {true}. We note
that if the streams underlying the propositions in P ∪{q} are all well-defined in all
time steps of all models, then this distinction in a weak and a strong case becomes
unnecessary.
 w on the left hand side of the consequence
relation defined by formula (1) in Section 2.1.4 above, whereas it is rejected by
w on the left hand side of the consequence
relation defined by formula (1) in Section 2.1.4 above, whereas it is rejected by  s on
the right hand side. This asymmetry in the consequence relation ensures that an
implementation which propagates nil more freely will accept more models in the
antecedent and less models in the consequent making it strictly harder to satisfy formula
(1).
s on
the right hand side. This asymmetry in the consequence relation ensures that an
implementation which propagates nil more freely will accept more models in the
antecedent and less models in the consequent making it strictly harder to satisfy formula
(1).
 false,1
false,1 true,2
true,2 true.
true.
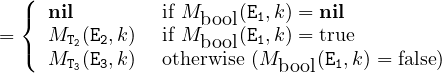
![{ MTE(E<i1:= V1,...in:= Vn>,k) if ∀j ∈ [1,n] : 0 ≤ Vj < Ej
= nil otherwise](HLL-LDD14x.png)
![{
= MTE(E<i1:= V1,...in:= Vn>,k) if ∀j ∈ [1,n] : Vj ∈ Tj
nil otherwise](HLL-LDD15x.png)
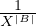
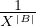 refers to integer division, which means that
this expression can only take the values −1, 0 or 1.
refers to integer division, which means that
this expression can only take the values −1, 0 or 1.
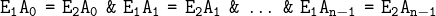











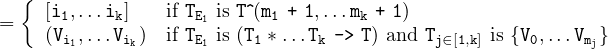
 if E1=Vn−1 then E(Vn−1) else E(Vn)
if E1=Vn−1 then E(Vn−1) else E(Vn)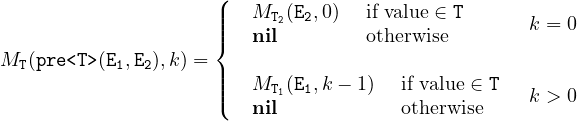
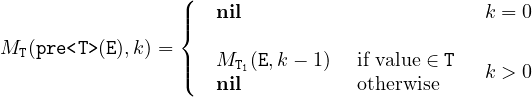
 (if En then 1 else 0)) < K
(if En then 1 else 0)) < K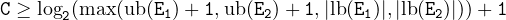
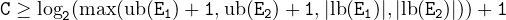
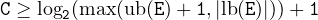
![(
|| .i if TEA is tuple {T0,...Tn− 1}
{ .Mi if TEA is struct {M0 : T0,...Mn−1 : Tn−1}
Ai = || [i] if TEA is T^(n)
( (Vi) if TEA is (T1-> T) and T1 is {V0,...Vn−1} with Vi < Vi+1](HLL-LDD39x.png)










![{ [i1,...ik] if TE is T^(m1 + 1,...mk + 1)
= (Vi,...Vi) if TEAis (T1 ∗ ...Tk -> T),T is {V0,...Vm },Vi < Vi+1
1 k A j∈[1,k] j](HLL-LDD50x.png)
![( ′ ′ ′
|||| Rij if Ri1...ij−1 is {R0,...Rmj}
||||
|||| Ri1...ip[ip+1,...ik] if j = k and Ri1...ip−1 is <collection> and
{ Ri1...ip is <expr> of type T^(mp+1 + 1,...mk + 1)
= ||
|||| Ri1...ip(Vip+1,...Vik) if j = k and Ri1...ip−1 is <collection> and
|||| Ri1...ip is <expr> of type (Tp+1 ∗...Tk-> T)
||(
undefined otherwise](HLL-LDD51x.png)



 |Pm1, Pm2, … Pmn => Rm)
|Pm1, Pm2, … Pmn => Rm)








![{ [i1,...in] if TE is T^(m1 + 1,...mn + 1)
= (Vi ,...Vi ) if TE is (T1 ∗ ...Tn -> T),T is {V0,...Vm }
1 n j∈[1,n] j](HLL-LDD65x.png)